| Date | May 2011 | Marks available | 2 | Reference code | 11M.2.sl.TZ1.8 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Show that | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows a waterwheel with a bucket. The wheel rotates at a constant rate in an anticlockwise (counter-clockwise) direction.
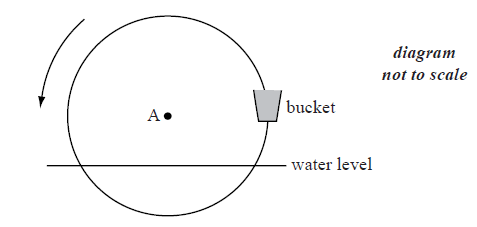
The diameter of the wheel is 8 metres. The centre of the wheel, A, is 2 metres above the water level. After t seconds, the height of the bucket above the water level is given by \(h = a\sin bt + 2\) .
Show that \(a = 4\) .
The wheel turns at a rate of one rotation every 30 seconds.
Show that \(b = \frac{\pi }{{15}}\) .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ - 1}}\) .
Find these values of t .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ - 1}}\) .
Determine whether the bucket is underwater at the second value of t .
Markscheme
METHOD 1
evidence of recognizing the amplitude is the radius (M1)
e.g. amplitude is half the diameter
\(a = \frac{8}{2}\) A1
\(a = 4\) AG N0
METHOD 2
evidence of recognizing the maximum height (M1)
e.g. \(h = 6\) , \(a\sin bt + 2 = 6\)
correct reasoning
e.g. \(a\sin bt = 4\) and \(\sin bt\) has amplitude of 1 A1
\(a = 4\) AG N0
[2 marks]
METHOD 1
period = 30 (A1)
\(b = \frac{{2\pi }}{{30}}\) A1
\(b = \frac{\pi }{{15}}\) AG N0
METHOD 2
correct equation (A1)
e.g. \(2 = 4\sin 30b + 2\) , \(\sin 30b = 0\)
\(30b = 2\pi \) A1
\(b = \frac{\pi }{{15}}\) AG N0
[2 marks]
recognizing \(h'(t) = - 0.5\) (seen anywhere) R1
attempting to solve (M1)
e.g. sketch of \(h'\) , finding \(h'\)
correct work involving \(h'\) A2
e.g. sketch of \(h'\) showing intersection, \( - 0.5 = \frac{{4\pi }}{{15}}\cos \left( {\frac{\pi }{{15}}t} \right)\)
\(t = 10.6\) , \(t = 19.4\) A1A1 N3
[6 marks]
METHOD 1
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of substituting into h (M1)
e.g. \(h(19.4)\) , \(4\sin \frac{{19.4\pi }}{{15}} + 2\)
correct calculation A1
e.g. \(h(19.4) = - 1.19\)
correct statement A1 N0
e.g. the bucket is underwater, yes
METHOD 2
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of valid approach (M1)
e.g. solving \(h(t) = 0\) , graph showing region below x-axis
correct roots A1
e.g. \(17.5\), \(27.5\)
correct statement A1 N0
e.g. the bucket is underwater, yes
[4 marks]
Examiners report
Parts (a) and (b) were generally well done.
Parts (a) and (b) were generally well done, however there were several instances of candidates working backwards from the given answer in part (b).
Parts (c) and (d) proved to be quite challenging for a large proportion of candidates. Many did not attempt these parts. The most common error was a misinterpretation of the word "descending" where numerous candidates took \(h'(t)\) to be 0.5 instead of \( - 0.5\) but incorrect derivatives for h were also widespread. The process required to solve for t from the equation \( - 0.5 = \frac{{4\pi }}{{15}}\cos \left( {\frac{\pi }{{15}}t} \right)\) overwhelmed those who attempted algebraic methods. Few could obtain both correct solutions, more had one correct while others included unreasonable values including \(t < 0\) .
In part (d), not many understood that the condition for underwater was \(h(t) < 0\) and had trouble interpreting the meaning of "second value". Many candidates, however, did recover to gain some marks in follow through.

