| Date | May 2016 | Marks available | 3 | Reference code | 16M.1.sl.TZ1.3 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find and Write down | Question number | 3 | Adapted from | N/A |
Question
Let \(f(x) = 3\sin \left( {\frac{\pi }{2}x} \right)\), for \(0 \leqslant x \leqslant 4\).
(i) Write down the amplitude of \(f\).
(ii) Find the period of \(f\).
On the following grid sketch the graph of \(f\).
Markscheme
(i) 3 A1 N1
(ii) valid attempt to find the period (M1)
eg\(\,\,\,\,\,\)\(\frac{{2\pi }}{b},{\text{ }}\frac{{2\pi }}{{\frac{\pi }{2}}}\)
period \( = 4\) A1 N2
[3 marks]
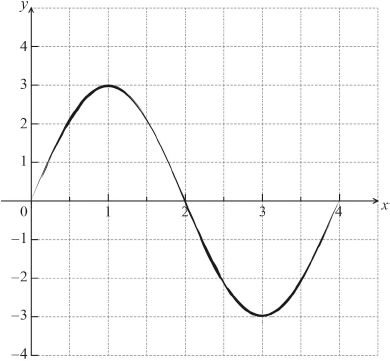A1A1A1A1 N4
[4 marks]
Examiners report
Almost all candidates correctly stated the amplitude but then had difficulty finding the correct period. Few students faced problems in sketching the graph of the given function, even if they had found the wrong period, thus indicating a lack of understanding of the term ‘period’ in part a(ii). Most sketches were good although care should be taken to observe the given domain and to draw a neat curve.
Almost all candidates correctly stated the amplitude but then had difficulty finding the correct period. Few students faced problems in sketching the graph of the given function, even if they had found the wrong period, thus indicating a lack of understanding of the term ‘period’ in part a(ii). Most sketches were good although care should be taken to observe the given domain and to draw a neat curve.
