| Date | November 2011 | Marks available | 3 | Reference code | 11N.1.sl.TZ0.9 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down | Question number | 9 | Adapted from | N/A |
Question
The following diagram shows the graph of \(f(x) = a\sin (b(x - c)) + d\) , for \(2 \le x \le 10\) .
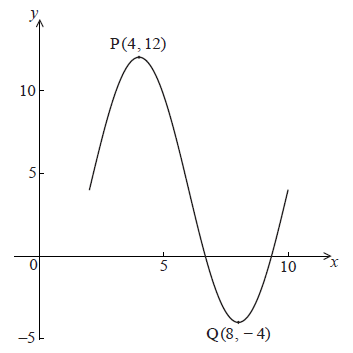
There is a maximum point at P(4, 12) and a minimum point at Q(8, −4) .
Use the graph to write down the value of
(i) a ;
(ii) c ;
(iii) d .
Show that \(b = \frac{\pi }{4}\) .
Find \(f'(x)\) .
At a point R, the gradient is \( - 2\pi \) . Find the x-coordinate of R.
Markscheme
(i) \(a = 8\) A1 N1
(ii) \(c = 2\) A1 N1
(iii) \(d = 4\) A1 N1
[3 marks]
METHOD 1
recognizing that period \( = 8\) (A1)
correct working A1
e.g. \(8 = \frac{{2\pi }}{b}\) , \(b = \frac{{2\pi }}{8}\)
\(b = \frac{\pi }{4}\) AG N0
METHOD 2
attempt to substitute M1
e.g. \(12 = 8\sin (b(4 - 2)) + 4\)
correct working A1
e.g. \(\sin 2b = 1\)
\(b = \frac{\pi }{4}\) AG N0
[2 marks]
evidence of attempt to differentiate or choosing chain rule (M1)
e.g. \(\cos \frac{\pi }{4}(x - 2)\) , \(\frac{\pi }{4} \times 8\)
\(f'(x) = 2\pi \cos \left( {\frac{\pi }{4}(x - 2)} \right)\) (accept \(2\pi \cos \frac{\pi }{4}(x - 2)\) ) A2 N3
[3 marks]
recognizing that gradient is \(f'(x)\) (M1)
e.g. \(f'(x) = m\)
correct equation A1
e.g. \( - 2\pi = 2\pi \cos \left( {\frac{\pi }{4}(x - 2)} \right)\) , \( - 1 = \cos \left( {\frac{\pi }{4}(x - 2)} \right)\)
correct working (A1)
e.g. \({\cos ^{ - 1}}( - 1) = \frac{\pi }{4}(x - 2)\)
using \({\cos ^{ - 1}}( - 1) = \pi \) (seen anywhere) (A1)
e.g. \(\pi = \frac{\pi }{4}(x - 2)\)
simplifying (A1)
e.g. \(4 = (x - 2)\)
\(x = 6\) A1 N4
[6 marks]
Examiners report
Part (a) of this question proved challenging for most candidates.
Although a good number of candidates recognized that the period was 8 in part (b), there were some who did not seem to realize that this period could be found using the given coordinates of the maximum and minimum points.
In part (c), not many candidates found the correct derivative using the chain rule.
For part (d), a good number of candidates correctly set their expression equal to \( - 2\pi \) , but errors in their previous values kept most from correctly solving the equation. Most candidates who had the correct equation were able to gain full marks here.

