| Date | May 2011 | Marks available | 3 | Reference code | 11M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Sketch | Question number | 10 | Adapted from | N/A |
Question
The following diagram represents a large Ferris wheel, with a diameter of 100 metres.
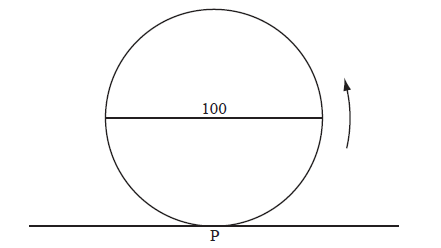
Let P be a point on the wheel. The wheel starts with P at the lowest point, at ground level. The wheel rotates at a constant rate, in an anticlockwise (counter-clockwise) direction. One revolution takes 20 minutes.
Let \(h(t)\) metres be the height of P above ground level after t minutes. Some values of \(h(t)\) are given in the table below.
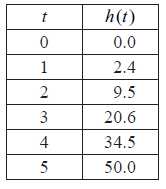
Write down the height of P above ground level after
(i) 10 minutes;
(ii) 15 minutes.
(i) Show that \(h(8) = 90.5\).
(ii) Find \(h(21)\) .
Sketch the graph of h , for \(0 \le t \le 40\) .
Given that h can be expressed in the form \(h(t) = a\cos bt + c\) , find a , b and c .
Markscheme
(i) 100 (metres) A1 N1
(ii) 50 (metres) A1 N1
[2 marks]
(i) identifying symmetry with \(h(2) = 9.5\) (M1)
subtraction A1
e.g. \(100 - h(2)\) , \(100 - 9.5\)
\(h(8) = 90.5\) AG N0
(ii) recognizing period (M1)
e.g. \(h(21) = h(1)\)
\(h(21) = 2.4\) A1 N2
[4 marks]
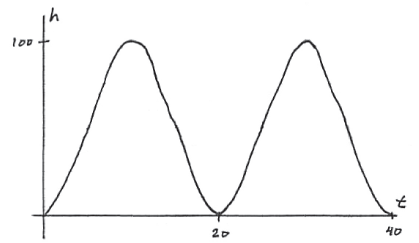 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for end points (0, 0) and (40, 0) , A1 for range \(0 \le h \le 100\) , A1 for approximately correct sinusoidal shape, with two cycles.
[3 marks]
evidence of a quotient involving 20, \(2\pi \) or \({360^ \circ }\) to find b (M1)
e.g. \(\frac{{2\pi }}{b} = 20\) , \(b = \frac{{360}}{{20}}\)
\(b = \frac{{2\pi }}{{20}}\) \(\left( { = \frac{\pi }{{10}}} \right)\) (accept \(b = 18\) if working in degrees) A1 N2
\(a = - 50\) , \(c = 50\) A2A1 N3
[5 marks]
Examiners report
Nearly all candidates answered part (a) correctly, finding the height of the wheel at \(\frac{1}{2}\) and \(\frac{3}{4}\) of a revolution.
While many candidates were successful in part (b), there were many who tried to use right-angled triangles or find a function for height, rather than recognizing the symmetry of the wheel in its different positions and using the values given in the table.
In part (c), most candidates were able to sketch a somewhat accurate representation of the height of the wheel over two full cycles. However, it seems that many candidates are not familiar with the shape of a sinusoidal wave, as many of the candidates' graphs were constructed of line segments, rather than a curve.
For part (d), candidates were less successful in finding the parameters of the cosine function. Even candidates who drew accurate sketches were not always able to relate their sketch to the function. These candidates understood the context of the problem, that the position on the wheel goes up and down, but they did not relate this to a trigonometric function. Only a small number of candidates recognized that the value of a would be negative. Candidates should be aware that while working in degrees may be acceptable, the expectation is that radians will be used in these types of questions.

