| Date | November 2008 | Marks available | 3 | Reference code | 08N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Give a full geometric description | Question number | 10 | Adapted from | N/A |
Question
Let \(f(t) = a\cos b(t - c) + d\) , \(t \ge 0\) . Part of the graph of \(y = f(t)\) is given below.
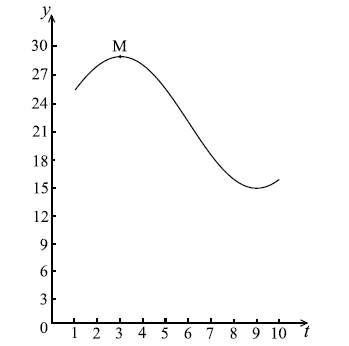
When \(t = 3\) , there is a maximum value of 29, at M.
When \(t = 9\) , there is a minimum value of 15.
(i) Find the value of a.
(ii) Show that \(b = \frac{\pi }{6}\) .
(iii) Find the value of d.
(iv) Write down a value for c.
The transformation P is given by a horizontal stretch of a scale factor of \(\frac{1}{2}\) , followed by a translation of \(\left( {\begin{array}{*{20}{c}}
3\\
{ - 10}
\end{array}} \right)\) .
Let \({M'}\) be the image of M under P. Find the coordinates of \({M'}\) .
The graph of g is the image of the graph of f under P.
Find \(g(t)\) in the form \(g(t) = 7\cos B(t - c) + D\) .
The graph of g is the image of the graph of f under P.
Give a full geometric description of the transformation that maps the graph of g to the graph of f .
Markscheme
(i) attempt to substitute (M1)
e.g. \(a = \frac{{29 - 15}}{2}\)
\(a = 7\) (accept \(a = - 7\) ) A1 N2
(ii) \({\text{period}} = 12\) (A1)
\(b = \frac{{2\pi }}{{12}}\) A1
\(b = \frac{\pi }{6}\) AG N0
(iii) attempt to substitute (M1)
e.g. \(d = \frac{{29 + 15}}{2}\)
\(d = 22\) A1 N2
(iv) \(c = 3\) (accept \(c = 9\) from \(a = - 7\) ) A1 N1
Note: Other correct values for c can be found, \(c = 3 \pm 12k\) , \(k \in \mathbb{Z}\) .
[7 marks]
stretch takes 3 to 1.5 (A1)
translation maps \((1.5{\text{, }}29)\) to \((4.5{\text{, }}19)\) (so \({M'}\) is \((4.5{\text{, }}19)\)) A1 N2
[2 marks]
\(g(t) = 7\cos \frac{\pi }{3}\left( {t - 4.5} \right) + 12\) A1A2A1 N4
Note: Award A1 for \(\frac{\pi }{3}\) , A2 for 4.5, A1 for 12.
Other correct values for c can be found, \(c = 4.5 \pm 6k\) , \(k \in \mathbb{Z}\) .
[4 marks]
translation \(\left( {\begin{array}{*{20}{c}}
{ - 3}\\
{10}
\end{array}} \right)\) (A1)
horizontal stretch of a scale factor of 2 (A1)
completely correct description, in correct order A1 N3
e.g. translation \(\left( {\begin{array}{*{20}{c}}
{ - 3}\\
{10}
\end{array}} \right)\) then horizontal stretch of a scale factor of 2
[3 marks]
Examiners report
This question was the most difficult on the paper. Where candidates attempted this question, part (a) was answered satisfactorily.
Few answered part (b) correctly as most could not interpret the horizontal stretch.
Few answered part (b) correctly as most could not interpret the horizontal stretch. As a result, there were many who were unable to answer part (c) although follow through marks were often obtained from incorrect answers in both parts (a) and (b). The link between the answer in (b) and the value of C in part (c) was lost on all but the most attentive.
In part (d), some candidates could name the transformations required, although only a handful provided the correct order of the transformations to return the graph to its original state.

