Question
The diagram below shows part of the graph of a function \(f\) .
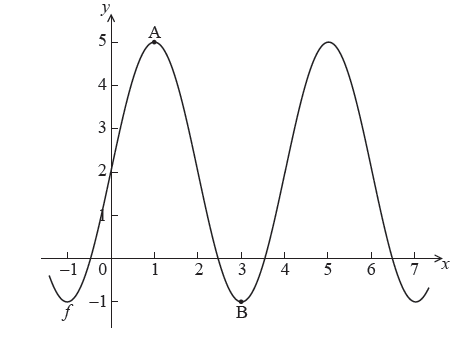
The graph has a maximum at A(\(1\), \(5\)) and a minimum at B(\(3\), \( -1\)) .
The function \(f\) can be written in the form \(f(x) = p\sin (qx) + r\) . Find the value of
(a) \(p\)
(b) \(q\)
(c) \(r\) .
[6]
.
Markscheme
(a) valid approach to find \(p\) (M1)
eg amplitude \( = \frac{{{\rm{max}} - {\rm{min}}}}{2}\) , \(p = 6\)
\(p = 3\) A1 N2
[2 marks]
(b) valid approach to find \(q\) (M1)
eg period = 4 , \(q = \frac{{2\pi }}{{{\rm{period}}}}\)
\(q = \frac{\pi }{2}\) A1 N2
[2 marks]
(c) valid approach to find \(r\) (M1)
eg axis = \(\frac{{{\rm{max}} + {\rm{min}}}}{2}\) , sketch of horizontal axis, \(f(0)\)
\(r = 2\) A1 N2
[2 marks]
Total [6 marks]
.
valid approach to find \(p\) (M1)
eg amplitude \( = \frac{{{\rm{max}} - {\rm{min}}}}{2}\) , \(p = 6\)
\(p = 3\) A1 N2
[2 marks]
a.
valid approach to find \(q\) (M1)
eg period = 4 , \(q = \frac{{2\pi }}{{{\rm{period}}}}\)
\(q = \frac{\pi }{2}\) A1 N2
[2 marks]
b.
valid approach to find \(r\) (M1)
eg axis = \(\frac{{{\rm{max}} + {\rm{min}}}}{2}\) , sketch of horizontal axis, \(f(0)\)
\(r = 2\) A1 N2
[2 marks]
Total [6 marks]
c.
Examiners report
Many candidates were able to answer all three parts of this question with no difficulty. Some candidates ran into problems when they attempted to substitute into the equation of the function with the parameters \(p\),\(q\) and \(r\). The successful candidates were able to find the answers using the given points and their understanding of the different transformations.
Part (b) seemed to be the most difficult, with some candidates not understanding the relationship between \(q\) and the period of the function. There were also some candidates who showed working such as\(\frac{{2\pi }}{b}\) without explaining what \(b\) represented.
.
Many candidates were able to answer all three parts of this question with no difficulty. Some candidates ran into problems when they attempted to substitute into the equation of the function with the parameters \(p\),\(q\) and \(r\). The successful candidates were able to find the answers using the given points and their understanding of the different transformations.
Part (b) seemed to be the most difficult, with some candidates not understanding the relationship between \(q\) and the period of the function. There were also some candidates who showed working such as\(\frac{{2\pi }}{b}\) without explaining what \(b\) represented.
a.
Many candidates were able to answer all three parts of this question with no difficulty. Some candidates ran into problems when they attempted to substitute into the equation of the function with the parameters \(p\),\(q\) and \(r\). The successful candidates were able to find the answers using the given points and their understanding of the different transformations.
Part (b) seemed to be the most difficult, with some candidates not understanding the relationship between \(q\) and the period of the function. There were also some candidates who showed working such as\(\frac{{2\pi }}{b}\) without explaining what \(b\) represented.
b.
Many candidates were able to answer all three parts of this question with no difficulty. Some candidates ran into problems when they attempted to substitute into the equation of the function with the parameters \(p\),\(q\) and \(r\). The successful candidates were able to find the answers using the given points and their understanding of the different transformations.
Part (b) seemed to be the most difficult, with some candidates not understanding the relationship between \(q\) and the period of the function. There were also some candidates who showed working such as\(\frac{{2\pi }}{b}\) without explaining what \(b\) represented.
c.
Syllabus sections


