| Date | November 2015 | Marks available | 2 | Reference code | 15N.1.sl.TZ0.4 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
Let \(f(x) = 3\sin (\pi x)\).
Write down the amplitude of \(f\).
[1]
a.
Find the period of \(f\).
[2]
b.
On the following grid, sketch the graph of \(y = f(x)\), for \(0 \le x \le 3\).
[4]
c.
Markscheme
amplitude is 3 A1 N1
a.
valid approach (M1)
eg\(\;\;\;{\text{period}} = \frac{{2\pi }}{\pi },{\text{ }}\frac{{360}}{\pi }\)
period is 2 A1 N2
b.
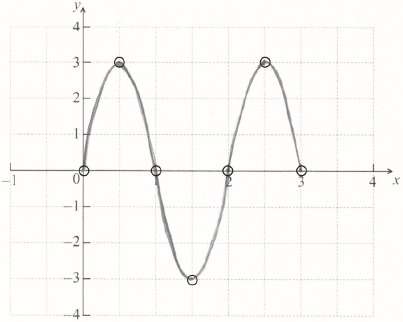 A1
A1
A1A1A1 N4
Note: Award A1 for sine curve starting at (0, 0) and correct period.
Only if this A1 is awarded, award the following for points in circles:
A1 for correct x-intercepts;
A1 for correct max and min points;
A1 for correct domain.
c.
Examiners report
[N/A]
a.
[N/A]
b.
[N/A]
c.
Syllabus sections
Topic 3 - Circular functions and trigonometry » 3.4 » The circular functions \(\sin x\) , \(\cos x\) and \(\tan x\) : their domains and ranges; amplitude, their periodic nature; and their graphs.
Show 59 related questions

