| Date | May 2017 | Marks available | 5 | Reference code | 17M.2.sl.TZ1.9 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
A random variable \(X\) is normally distributed with mean, \(\mu \). In the following diagram, the shaded region between 9 and \(\mu \) represents 30% of the distribution.
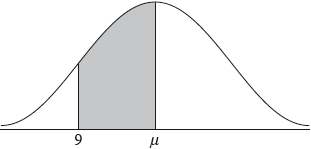
The standard deviation of \(X\) is 2.1.
The random variable \(Y\) is normally distributed with mean \(\lambda \) and standard deviation 3.5. The events \(X > 9\) and \(Y > 9\) are independent, and \(P\left( {(X > 9) \cap (Y > 9)} \right) = 0.4\).
Find \({\text{P}}(X < 9)\).
Find the value of \(\mu \).
Find \(\lambda \).
Given that \(Y > 9\), find \({\text{P}}(Y < 13)\).
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(X < \mu ) = 0.5,{\text{ }}0.5 - 0.3\)
\({\text{P}}(X < 9) = 0.2\) (exact) A1 N2
[2 marks]
\(z = - 0.841621\) (may be seen in equation) (A1)
valid attempt to set up an equation with their \(z\) (M1)
eg\(\,\,\,\,\,\)\( - 0.842 = \frac{{\mu - X}}{\sigma },{\text{ }} - 0.842 = \frac{{X - \mu }}{\sigma },{\text{ }}z = \frac{{9 - \mu }}{{2.1}}\)
10.7674
\(\mu = 10.8\) A1 N3
[3 marks]
\({\text{P}}(X > 9) = 0.8\) (seen anywhere) (A1)
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A) \times {\text{P}}(B)\)
correct equation (A1)
eg\(\,\,\,\,\,\)\(0.8 \times {\text{P}}(Y > 9) = 0.4\)
\({\text{P}}(Y > 9) = 0.5\) A1
\(\lambda = 9\) A1 N3
[5 marks]
finding \({\text{P}}(9 < Y < 13) = 0.373450\) (seen anywhere) (A2)
recognizing conditional probability (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A|B),{\text{ P}}(Y < 13|Y > 9)\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{0.373}}}}{{0.5}}\)
0.746901
0.747 A1 N3
[5 marks]

