| Date | May 2010 | Marks available | 4 | Reference code | 10M.1.sl.TZ2.9 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
José travels to school on a bus. On any day, the probability that José will miss the bus is \(\frac{1}{3}\) .
If he misses his bus, the probability that he will be late for school is \(\frac{7}{8}\) .
If he does not miss his bus, the probability that he will be late is \(\frac{3}{8}\) .
Let E be the event “he misses his bus” and F the event “he is late for school”.
The information above is shown on the following tree diagram.
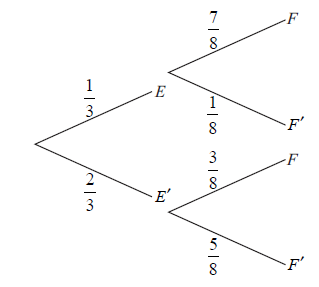
Find
(i) \({\rm{P}}(E \cap F)\) ;
(ii) \({\rm{P}}(F)\) .
Find the probability that
(i) José misses his bus and is not late for school;
(ii) José missed his bus, given that he is late for school.
The cost for each day that José catches the bus is 3 euros. José goes to school on Monday and Tuesday.
Copy and complete the probability distribution table.

The cost for each day that José catches the bus is 3 euros. José goes to school on Monday and Tuesday.
Find the expected cost for José for both days.
Markscheme
(i) \(\frac{7}{{24}}\) A1 N1
(ii) evidence of multiplying along the branches (M1)
e.g. \(\frac{2}{3} \times \frac{5}{8}\) , \(\frac{1}{3} \times \frac{7}{8}\)
adding probabilities of two mutually exclusive paths (M1)
e.g. \(\left( {\frac{1}{3} \times \frac{7}{8}} \right) + \left( {\frac{2}{3} \times \frac{3}{8}} \right)\) , \(\left( {\frac{1}{3} \times \frac{1}{8}} \right) + \left( {\frac{2}{3} \times \frac{5}{8}} \right)\)
\({\rm{P}}(F) = \frac{{13}}{{24}}\) A1 N2
[4 marks]
(i) \(\frac{1}{3} \times \frac{1}{8}\) (A1)
\(\frac{1}{{24}}\) A1
(ii) recognizing this is \({\rm{P}}(E|F)\) (M1)
e.g. \(\frac{7}{{24}} \div \frac{{13}}{{24}}\)
\(\frac{{168}}{{312}}\) \(\left( { = \frac{7}{{13}}} \right)\) A2 N3
[5 marks]
 A2A1 N3
A2A1 N3
[3 marks]
correct substitution into \({\rm{E}}(X)\) formula (M1)
e.g. \(0 \times \frac{1}{9} + 3 \times \frac{4}{9} + 6 \times \frac{4}{9}\) , \(\frac{{12}}{9} + \frac{{24}}{9}\)
\({\rm{E}}(X) = 4\) (euros) A1 N2
[2 marks]
Examiners report
Candidates generally handled some or all of parts (a) and (b) well. Errors included adding probabilities along branches and trying to use the union formula from the information booklet.
Candidates generally handled some or all of parts (a) and (b) well. Errors included adding probabilities along branches and trying to use the union formula from the information booklet. On part (b)(ii), many candidates knew that they were supposed to use some type of conditional probability but did not know how to find \({\rm{P}}(E|F)\) . Many candidates made errors working with fractions. Some candidates who missed part (a)(ii) were able to earn follow-through credit on part (b)(ii).
Many candidates had difficulty completing the probability distribution table. While the common error of finding the probability for \(x = 3\) as \(\frac{2}{9}\) was understandable as the candidate did not appreciate that there were two ways of paying three euros, it was disappointing that these candidates often correctly found \({\rm{P}}(X = 4)\) as \(\frac{4}{9}\) and did not note that the probabilities failed to sum to one. These candidates could not earn full follow-through marks on their expected value calculation in part (d). Some candidates did use the probabilities summing to one with incorrect probabilities in part (c); these candidates often earned full follow-through marks in part (d), as a majority of candidates knew the method for finding expected value.
Many candidates had difficulty completing the probability distribution table. While the common error of finding the probability for \(x = 3\) as \(\frac{2}{9}\) was understandable as the candidate did not appreciate that there were two ways of paying three Euros, it was disappointing that these candidates often correctly found \({\rm{P}}(X) = 4\) as \(\frac{4}{9}\) and did not note that the probabilities failed to sum to one. These candidates could not earn full follow-through marks on their expected value calculation in part (d). Some candidates did use the probabilities summing to one with incorrect probabilities in part (c); these candidates often earned full follow-through marks in part (d), as a majority of candidates knew the method for finding expected value.

