| Date | November 2010 | Marks available | 3 | Reference code | 10N.1.sl.TZ0.4 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The diagram below shows the probabilities for events A and B , with \({\rm{P}}(A') = p\) .
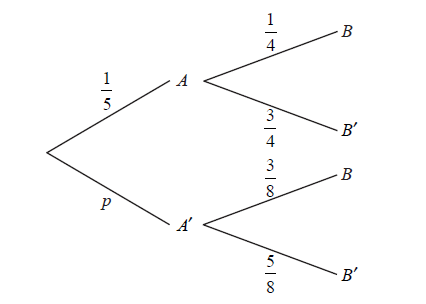
Write down the value of p .
Find \({\rm{P}}(B)\) .
Find \({\rm{P}}(A'|B)\) .
Markscheme
\(p = \frac{4}{5}\) A1 N1
[1 mark]
multiplying along the branches (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4}\) , \(\frac{{12}}{{40}}\)
adding products of probabilities of two mutually exclusive paths (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4} + \frac{4}{5} \times \frac{3}{8}\) , \(\frac{1}{{20}} + \frac{{12}}{{40}}\)
\({\rm{P}}(B) = \frac{{14}}{{40}}\) \(\left( { = \frac{7}{{20}}} \right)\) A1 N2
[3 marks]
appropriate approach which must include \({A'}\) (may be seen on diagram) (M1)
e.g. \(\frac{{{\rm{P}}(A' \cap B)}}{{{\rm{P}}(B)}}\) (do not accept \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) )
\({\rm{P}}(A'|B) = \frac{{\frac{4}{5} \times \frac{3}{8}}}{{\frac{7}{{20}}}}\) (A1)
\({\rm{P}}(A'|B) = \frac{{12}}{{14}}\) \(\left( { = \frac{6}{7}} \right)\) A1 N2
[3 marks]
Examiners report
While nearly every candidate answered part (a) correctly, many had trouble with the other parts of this question.
In part (b), many candidates did not multiply along the branches of the tree diagram to find the required values, and many did not realize that there were two paths for P(B). There were also many candidates who understood what the question required, but then did not know how to multiply fractions correctly, and these calculation errors led to an incorrect answer.
In part (c), most candidates attempted to use a formula for conditional probability found in the information booklet, but very few substituted the correct values.

