| Date | May 2012 | Marks available | 5 | Reference code | 12M.1.sl.TZ2.9 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find and Copy and complete | Question number | 9 | Adapted from | N/A |
Question
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
(i) Copy and complete the following tree diagram.
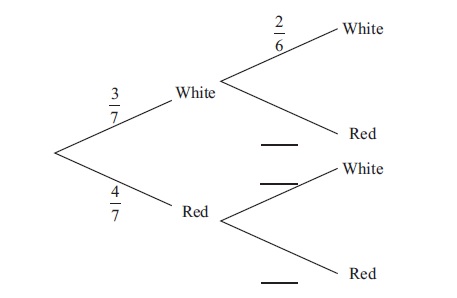
(ii) Find the probability that two white balls are chosen.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Find the probability that the two balls are white.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Given that both balls are white, find the probability that they were chosen from bag A.
Markscheme
(i)
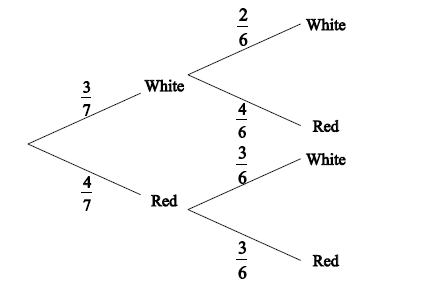
\(\frac{4}{6},\frac{3}{6}{\rm{and}}\frac{3}{6}\left( {\frac{2}{3},\frac{1}{2}{\rm{and}}\frac{1}{2}} \right)\) A1A1A1 N3
(ii) multiplying along the correct branches (may be seen on diagram) (A1)
e.g. \(\frac{3}{7} \times \frac{2}{6}\)
\(\frac{6}{{42}}\left( { = \frac{1}{7}} \right)\) A1 N2
[5 marks]
\({\rm{P(bag A) = }}\frac{2}{6}\left( { = \frac{1}{3}} \right)\) , \({\rm{P(bag B) = }}\frac{4}{6}\left( { = \frac{2}{3}} \right)\) (seen anywhere) (A1)(A1)
appropriate approach (M1)
e.g. \({\rm{P(}}WW \cap A) + {\rm{P}}(WW \cap B)\)
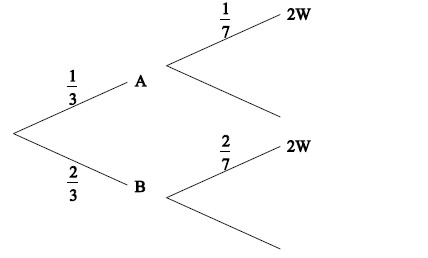
correct calculation A1
e.g. \(\frac{1}{3} \times \frac{1}{7} + \frac{2}{3} \times \frac{2}{7}\) , \(\frac{2}{{42}} + \frac{8}{{42}}\)
\({\rm{P}}(2W) = \frac{{60}}{{252}}\left( { = \frac{5}{{21}}} \right)\) A1 N3
[5 marks]
recognizing conditional probability (M1)
e.g. \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) , \({\rm{P}}(A|WW) = \frac{{{\rm{P}}(WW \cap A)}}{{{\rm{P}}(WW)}}\)
correct numerator (A1)
e.g. \({\rm{P}}(A \cap WW) = \frac{6}{{42}} \times \frac{2}{6},\frac{1}{{21}}\)
correct denominator (A1)
e.g. \(\frac{6}{{252}},\frac{5}{{21}}\)
probability \(\frac{{84}}{{420}}\left( { = \frac{1}{5}} \right)\) A1 N3
[4 marks]
Examiners report
Part (a) of this question was answered correctly by the large majority of candidates. There were some who did not follow the instruction to copy and complete the tree diagram on their separate paper, and simply filled in the blanks on the exam paper.
In part (b), many candidates struggled with finding the compound probability, and did not use the provided information in the appropriate manner. Quite a few candidates seemed to be confused about when they should add the probabilities or when they should multiply.
In part (c), many recognized that the question dealt with conditional probability, and many tried to use the formula from the information booklet, but failed to realize that they had already found the required values for the numerator and denominator in their working for part (b).
Throughout this question, it was discouraging to see the large number of candidates making arithmetic errors. There were a surprising number of candidates who multiplied fractions incorrectly, or found an incorrect value for simple multiplication such as \(2 \times 4 = 6\) or \(6 \times 7 = 43\) .

