| Date | May 2011 | Marks available | 5 | Reference code | 11M.1.sl.TZ1.8 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find and Write down | Question number | 8 | Adapted from | N/A |
Question
In a group of 16 students, 12 take art and 8 take music. One student takes neither art nor music. The Venn diagram below shows the events art and music. The values p , q , r and s represent numbers of students.
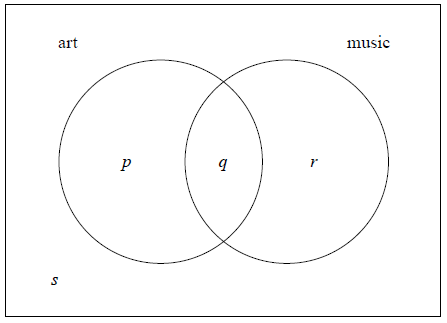
(i) Write down the value of s .
(ii) Find the value of q .
(iii) Write down the value of p and of r .
(i) A student is selected at random. Given that the student takes music, write down the probability the student takes art.
(ii) Hence, show that taking music and taking art are not independent events.
Two students are selected at random, one after the other. Find the probability that the first student takes only music and the second student takes only art.
Markscheme
(i) \(s = 1\) A1 N1
(ii) evidence of appropriate approach (M1)
e.g. \(21 - 16\) , \(12 + 8 - q = 15\)
\(q = 5\) A1 N2
(iii) \(p = 7\) , \(r = 3\) A1A1 N2
[5 marks]
(i) \({\rm{P(art|music)}} = \frac{5}{8}\) A2 N2
(ii) METHOD 1
\({\rm{P(art)}} = \frac{{12}}{{16}}\) \(\left( { = \frac{3}{4}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{3}{4} \ne \frac{5}{8}\)
the events are not independent AG N0
METHOD 2
\({\rm{P(art)}} \times {\rm{P(music)}} = \frac{{96}}{{256}}\) \(\left( { = \frac{3}{8}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{{12}}{{16}} \times \frac{8}{{16}} \ne \frac{5}{{16}}\)
the events are not independent AG N0
[4 marks]
\({\text{P(first takes only music)}} = \frac{3}{{16}}\) (seen anywhere) A1
\({\text{P(second takes only art)}} = \frac{7}{{15}}\) (seen anywhere) A1
evidence of valid approach (M1)
e.g. \(\frac{3}{{16}} \times \frac{7}{{15}}\)
\({\text{P(music and art)}} = \frac{{21}}{{240}}\) \(\left( { = \frac{7}{{80}}} \right)\) A1 N2
[4 marks]
Examiners report
A majority of candidates found the values in the Venn diagram easily. Common errors include giving \(s = 16\) , and also neglecting s in finding \(q = 4\) (e.g. \(12 + 8 - 16\) ) . Some interpreted the values as probabilities, despite the question explicitly stating that p, q, r and s represent numbers of students. Occasionally the values for p and r were misinterpreted as being inclusive of q. Follow-through marks were often earned in subsequent parts for such cases.
For (b), rather than think of the situations conceptually, most candidates reached for the formula for conditional probability, with mixed results. Few candidates considered that independence means \({\rm{P}}(A|M) = {\rm{P}}(A)\) . Most applied \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B)\) , with many giving incomplete or incorrect calculations. Some candidates compared the wrong things and showed, for example, that \(\frac{5}{8} \ne \frac{3}{8}\) , which incorrectly compares \({\rm{P}}(A|M)\) with \({\rm{P}}(A \cap M)\) . Others stated that because there is an intersection, the events are independent, which is an insufficient explanation.
Part (c) was commonly answered as if there is replacement, with many candidates calculating \(\frac{3}{{16}} \times \frac{7}{{16}}\) . However, implicit in the phrasing "one after the other" is that there is no replacement.

