| Date | May 2012 | Marks available | 3 | Reference code | 12M.1.sl.TZ1.4 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find and Write down | Question number | 4 | Adapted from | N/A |
Question
Events A and B are such that \({\rm{P}}(A) = 0.3\) , \({\rm{P}}(B) = 0.6\) and \({\rm{P}}(A \cup B) = 0.7\) .
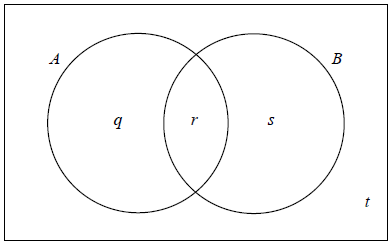
The values q , r , s and t represent probabilities.
Write down the value of t .
(i) Show that \(r = 0.2\) .
(ii) Write down the value of q and of s .
(i) Write down \({\rm{P}}(B')\) .
(ii) Find \({\rm{P}}(A|B')\) .
Markscheme
\(t = 0.3\) A1 N1
[1 mark]
(i) correct values A1
e.g. \(0.3 + 0.6 - 0.7\) , \(0.9 - 0.7\)
\(r = 0.2\) AG N0
(ii) \(q = 0.1\) , \(s = 0.4\) A1A1 N2
[3 marks]
(i) \(0.4\) A1 N1
(ii) \({\rm{P}}(A|B') = \frac{1}{4}\) A2 N2
[3 marks]
Examiners report
Parts (a), (b), and (c)(i) of this Venn diagram probability question were answered quite well with candidates consistently earning full marks.
Parts (a), (b), and (c)(i) of this Venn diagram probability question were answered quite well with candidates consistently earning full marks. Only a few candidates worked backwards from the \(r = 0.2\) given in the "show that" portion of part (b).
Many candidates struggled on part (c)(ii), either not recognizing conditional probability or multiplying probabilities to find the numerator as if the events were independent. A number of candidates who successfully found the probability in part (c)(ii) left their incomplete answer of \(\frac{{0.1}}{{0.4}}\) .

