| Date | November 2014 | Marks available | 2 | Reference code | 14N.1.sl.TZ0.8 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
Adam travels to school by car (\(C\)) or by bicycle (\(B\)). On any particular day he is equally likely to travel by car or by bicycle.
The probability of being late (\(L\)) for school is \(\frac{1}{6}\) if he travels by car.
The probability of being late for school is \(\frac{1}{3}\) if he travels by bicycle.
This information is represented by the following tree diagram.
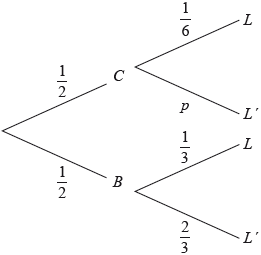
Find the value of \(p\).
Find the probability that Adam will travel by car and be late for school.
Find the probability that Adam will be late for school.
Given that Adam is late for school, find the probability that he travelled by car.
Adam will go to school three times next week.
Find the probability that Adam will be late exactly once.
Markscheme
correct working (A1)
eg\(\;\;\;1 - \frac{1}{6}\)
\(p = \frac{5}{6}\) A1 N2
[2 marks]
multiplying along correct branches (A1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6}\)
\({\text{P}}(C \cap L) = \frac{1}{{12}}\) A1 N2
[2 marks]
multiplying along the other branch (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{3}\)
adding probabilities of their \(2\) mutually exclusive paths (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6} + \frac{1}{2} \times \frac{1}{3}\)
correct working (A1)
eg\(\;\;\;\frac{1}{{12}} + \frac{1}{6}\)
\({\text{P}}(L) = \frac{3}{{12}}\;\;\;\left( { = \frac{1}{4}} \right)\) A1 N3
[4 marks]
recognizing conditional probability (seen anywhere) (M1)
eg\(\;\;\;{\text{P}}(C|L)\)
correct substitution of their values into formula (A1)
eg\(\frac{{\frac{1}{{12}}}}{{\frac{3}{{12}}}}\)
\({\text{P}}(C|L) = \frac{1}{3}\) A1 N2
[3 marks]
valid approach (M1)
eg \(X \sim B\) \(\left({3,{\text{ }}\frac{1}{4}} \right),{\text{ }}\left({\frac{1}{4}} \right){\left({\frac{3}{4}} \right)^2},{\text{ }}\left( {\begin{array}{*{20}{c}}3 \\1\end{array}} \right)\), three ways it could happen
correct substitution (A1)
eg \(\;\;\;\left({\begin{array}{*{20}{c}}3\\1\end{array}}\right){\left({\frac{1}{4}}\right)^1}{\left({\frac{3}{4}} \right)^2},{\text{ }}\frac{1}{4}\times\frac{3}{4}\times\frac{3}{4} + \frac{3}{4} \times\frac{1}{4}\times\frac{3}{4} + \frac{3}{4}\times\frac{3}{4}\times\frac{1}{4}\)
correct working (A1)
eg\(\;\;\;3\left( {\frac{1}{4}} \right)\left( {\frac{9}{{16}}} \right),{\text{ }}\frac{9}{{64}} + \frac{9}{{64}} + \frac{9}{{64}}\)
\(\frac{{27}}{{64}}\) A1 N2
[4 marks]
Total [15 marks]
Examiners report
Parts (a) and (b) of this question were answered correctly by nearly all candidates, and the majority earned full marks on part (c), as well. Unfortunately, there were a number of candidates who made arithmetic errors when multiplying or adding fractions.
Parts (a) and (b) of this question were answered correctly by nearly all candidates, and the majority earned full marks on part (c), as well. Unfortunately, there were a number of candidates who made arithmetic errors when multiplying or adding fractions. Candidates were not as successful in parts (d) and (e) of this question. Although many knew that conditional probability was necessary in part (d), many did not know to use their values from parts (b) and (c), and started from scratch with brand new, and often incorrect, calculations for the numerator and denominator. A majority of candidates did not recognize that binomial probability was needed in part (e), not realizing that there were three ways for Adam to be "late exactly once". A very common incorrect solution to part (e) was \(\frac{1}{4} \times \frac{3}{4} \times \frac{3}{4} = \frac{9}{{64}}\).
Parts (a) and (b) of this question were answered correctly by nearly all candidates, and the majority earned full marks on part (c), as well. Unfortunately, there were a number of candidates who made arithmetic errors when multiplying or adding fractions. Candidates were not as successful in parts (d) and (e) of this question. Although many knew that conditional probability was necessary in part (d), many did not know to use their values from parts (b) and (c), and started from scratch with brand new, and often incorrect, calculations for the numerator and denominator. A majority of candidates did not recognize that binomial probability was needed in part (e), not realizing that there were three ways for Adam to be "late exactly once". A very common incorrect solution to part (e) was \(\frac{1}{4} \times \frac{3}{4} \times \frac{3}{4} = \frac{9}{{64}}\).
Parts (a) and (b) of this question were answered correctly by nearly all candidates, and the majority earned full marks on part (c), as well. Unfortunately, there were a number of candidates who made arithmetic errors when multiplying or adding fractions. Candidates were not as successful in parts (d) and (e) of this question. Although many knew that conditional probability was necessary in part (d), many did not know to use their values from parts (b) and (c), and started from scratch with brand new, and often incorrect, calculations for the numerator and denominator. A majority of candidates did not recognize that binomial probability was needed in part (e), not realizing that there were three ways for Adam to be "late exactly once". A very common incorrect solution to part (e) was \(\frac{1}{4} \times \frac{3}{4} \times \frac{3}{4} = \frac{9}{{64}}\).
Parts (a) and (b) of this question were answered correctly by nearly all candidates, and the majority earned full marks on part (c), as well. Unfortunately, there were a number of candidates who made arithmetic errors when multiplying or adding fractions. Candidates were not as successful in parts (d) and (e) of this question. Although many knew that conditional probability was necessary in part (d), many did not know to use their values from parts (b) and (c), and started from scratch with brand new, and often incorrect, calculations for the numerator and denominator. A majority of candidates did not recognize that binomial probability was needed in part (e), not realizing that there were three ways for Adam to be "late exactly once". A very common incorrect solution to part (e) was \(\frac{1}{4}\times\frac{3}{4} \times\frac{3}{4} = \frac{9}{{64}}\).

