| Date | May 2010 | Marks available | 3 | Reference code | 10M.1.sl.TZ1.5 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Write down | Question number | 5 | Adapted from | N/A |
Question
Consider the events A and B, where \({\rm{P}}(A) = 0.5\) , \({\rm{P}}(B) = 0.7\) and \({\rm{P}}(A \cap B) = 0.3\) .
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
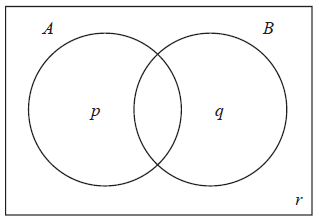
Write down the value of
(i) p ;
(ii) q ;
(iii) r.
Find the value of \({\rm{P}}(A|B')\) .
Hence, or otherwise, show that the events A and B are not independent.
Markscheme
(i) \(p = 0.2\) A1 N1
(ii) \(q = 0.4\) A1 N1
(iii) \(r = 0.1\) A1 N1
[3 marks]
\({\rm{P}}(A|B') = \frac{2}{3}\) A2 N2
Note: Award A1 for an unfinished answer such as \(\frac{{0.2}}{{0.3}}\) .
[2 marks]
valid reason R1
e.g. \(\frac{2}{3} \ne 0.5\) , \(0.35 \ne 0.3\)
thus, A and B are not independent AG N0
[1 mark]
Examiners report
As the definitions of p and q were not clear to candidates, both responses of p \(= 0.2\), q \(= 0.4\) and p \(= 0.5\), q \(= 0.7\) were accepted for full marks. However, finding r eluded many.
Few candidates answered the conditional probability correctly. Many attempted to use the formula in the booklet without considering the complement, and there was little evidence of the Venn diagram being utilized as a helpful aid.
To show the events are not independent, many correctly reasoned that \(0.3 \ne 0.35\) . A handful recognized that \({\rm{P}}(A|B') \ne {\rm{P}}(A)\) is an alternative approach that uses the answer in part (b). Some candidates do not know the difference between independent and mutually exclusive.

