| Date | May 2016 | Marks available | 4 | Reference code | 16M.1.sl.TZ2.8 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Copy and complete and Write down | Question number | 8 | Adapted from | N/A |
Question
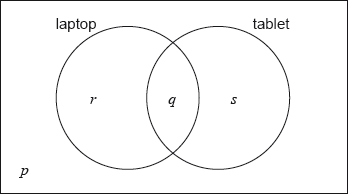
In a class of 21 students, 12 own a laptop, 10 own a tablet, and 3 own neither.
The following Venn diagram shows the events “own a laptop” and “own a tablet”.
The values \(p\), \(q\), \(r\) and \(s\) represent numbers of students.
A student is selected at random from the class.
Two students are randomly selected from the class. Let \(L\) be the event a “student owns a laptop”.
(i) Write down the value of \(p\).
(ii) Find the value of \(q\).
(iii) Write down the value of \(r\) and of \(s\).
(i) Write down the probability that this student owns a laptop.
(ii) Find the probability that this student owns a laptop or a tablet but not both.
(i) Copy and complete the following tree diagram. (Do not write on this page.)
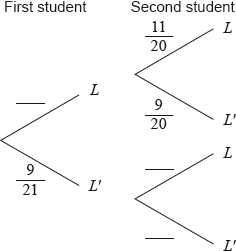
(ii) Write down the probability that the second student owns a laptop given that the first owns a laptop.
Markscheme
(i) \(p = 3\) A1 N1
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\((12 + 10 + 3) - 21,{\text{ }}22 - 18\)
\(q = 4\) A1 N2
(iii) \(r = 8,{\text{ }}s = 6\) A1A1 N2
(i) \(\frac{{12}}{{21}}{\text{ }}\left( { = \frac{4}{7}} \right)\) A2 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\(8 + 6,{\text{ }}r + s\)
\(\frac{{14}}{{21}}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1 N2
(i)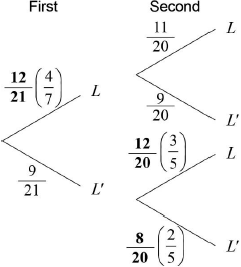 
A1A1A1 N3
(ii) \(\frac{{11}}{{20}}\) A1 N1
[4 marks]
Examiners report
On the whole, candidates were very successful on this question, with the majority of candidates earning most of the available marks.
On the whole, candidates were very successful on this question, with the majority of candidates earning most of the available marks.
On the whole, candidates were very successful on this question, with the majority of candidates earning most of the available marks. The most common error was seen in part (c)(ii), where many candidates did not earn the mark. It is also interesting to note that many of the candidates who answered this part correctly did so by using the formula for conditional probability, rather than recognizing that the required probability is given to them in the second branch of the tree diagram.
