| Date | November 2011 | Marks available | 2 | Reference code | 11N.2.sl.TZ0.9 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
A company produces a large number of water containers. Each container has two parts, a bottle and a cap. The bottles and caps are tested to check that they are not defective.
A cap has a probability of 0.012 of being defective. A random sample of 10 caps is selected for inspection.
Find the probability that exactly one cap in the sample will be defective.
The sample of caps passes inspection if at most one cap is defective. Find the probability that the sample passes inspection.
The heights of the bottles are normally distributed with a mean of \(22{\text{ cm}}\) and a standard deviation of \(0.3{\text{ cm}}\).
(i) Copy and complete the following diagram, shading the region representing where the heights are less than \(22.63{\text{ cm}}\).
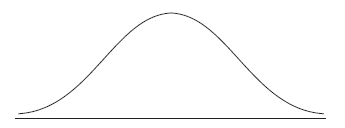
(ii) Find the probability that the height of a bottle is less than \(22.63{\text{ cm}}\).
(i) A bottle is accepted if its height lies between \(21.37{\text{ cm}}\) and \(22.63{\text{ cm}}\). Find the probability that a bottle selected at random is accepted.
(ii) A sample of 10 bottles passes inspection if all of the bottles in the sample are accepted. Find the probability that the sample passes inspection.
The bottles and caps are manufactured separately. A sample of 10 bottles and a sample of 10 caps are randomly selected for testing. Find the probability that both samples pass inspection.
Markscheme
Note: There may be slight differences in answers, depending on whether candidates use tables or GDCs, or their 3 sf answers in subsequent parts. Do not penalise answers that are consistent with their working and check carefully for FT.
evidence of recognizing binomial (seen anywhere in the question) (M1)
e.g. \(_n{C_r}{p^r}{q^{n - r}}\) , \({\text{B}}(n{\text{, }}p)\) , \(^{10}{C_1}{(0.012)^1}{(0.988)^9}\)
\(p = 0.108\) A1 N2
[2 marks]
valid approach (M1)
e.g. \({\rm{P}}(X \le 1)\) , \(0.88627 \ldots + 0.10764 \ldots \)
\(p = 0.994\) A1 N2
[2 marks]
(i)
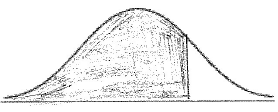 A1A1 N2
A1A1 N2
Note: Award A1 for vertical line to right of mean, A1 for shading to left of their vertical line.
(ii) valid approach (M1)
e.g. \({\rm{P}}(X < 22.63)\)
working to find standardized value (A1)
e.g. \(\frac{{22.63 - 22}}{{0.3}}\) , 2.1
\(p = 0.982\) A1 N3
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(21.37 < X < 22.63)\) , \({\rm{P}}( - 2.1 < z < 2.1)\)
correct working (A1)
e.g. \(0.982 - (1 - 0.982)\)
\(p = 0.964\) A1 N3
(ii) correct working (A1)
e.g. \(X \sim {\rm{B}}(10,0.964)\) , \({(0.964)^{10}}\)
\(p = 0.695\) (accept 0.694 from tables) A1 N2
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A){\rm{P}}(B)\) , \((0.994) \times {(0.964)^{10}}\)
\(p = 0.691\) (accept \(0.690\) from tables) A1 N2
[2 marks]
Examiners report
Many stronger candidates were completely successful with this question, employing technology efficiently. A number of candidates did not recognize the binomial probability in parts (a) and (b), and in part (b) a proportion of candidates just subtracted their part (a) answer from one. Candidates had more success with the normal distribution and many obtained follow-through marks in part (e) after an error made in part (b). Many candidates did not appreciate the independence in part (e) and added probabilities rather than multiplying them. A number of candidates were penalised for not giving their answers to 3 significant figures.
Many stronger candidates were completely successful with this question, employing technology efficiently. A number of candidates did not recognize the binomial probability in parts (a) and (b), and in part (b) a proportion of candidates just subtracted their part (a) answer from one. Candidates had more success with the normal distribution and many obtained follow-through marks in part (e) after an error made in part (b). Many candidates did not appreciate the independence in part (e) and added probabilities rather than multiplying them. A number of candidates were penalised for not giving their answers to 3 significant figures.
Many stronger candidates were completely successful with this question, employing technology efficiently. A number of candidates did not recognize the binomial probability in parts (a) and (b), and in part (b) a proportion of candidates just subtracted their part (a) answer from one. Candidates had more success with the normal distribution and many obtained follow-through marks in part (e) after an error made in part (b). Many candidates did not appreciate the independence in part (e) and added probabilities rather than multiplying them. A number of candidates were penalised for not giving their answers to 3 significant figures.
Many stronger candidates were completely successful with this question, employing technology efficiently. A number of candidates did not recognize the binomial probability in parts (a) and (b), and in part (b) a proportion of candidates just subtracted their part (a) answer from one. Candidates had more success with the normal distribution and many obtained follow-through marks in part (e) after an error made in part (b). Many candidates did not appreciate the independence in part (e) and added probabilities rather than multiplying them. A number of candidates were penalised for not giving their answers to 3 significant figures.
Many stronger candidates were completely successful with this question, employing technology efficiently. A number of candidates did not recognize the binomial probability in parts (a) and (b), and in part (b) a proportion of candidates just subtracted their part (a) answer from one. Candidates had more success with the normal distribution and many obtained follow-through marks in part (e) after an error made in part (b). Many candidates did not appreciate the independence in part (e) and added probabilities rather than multiplying them. A number of candidates were penalised for not giving their answers to 3 significant figures.

