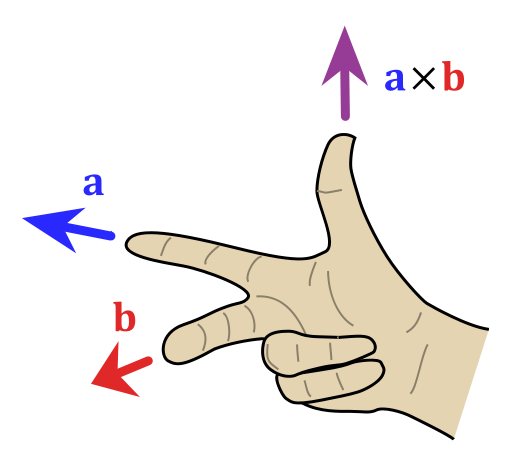
The vector product is a way of combining two vectors to find a third vector that is perpendicular to the first two. The vector product is a vector ! Don't mix it up with the scalar product which is a scalar! The vector product is useful for finding the equation of a plane . The properties are important, so learn them. The two following formula give the definition of the vector product
\(\textbf{v}\times \textbf{w}=\left( \begin{matrix} { \textbf{v} }_{ 1 } \\ { \textbf{v} }_{ 2 } \\ { \textbf{v} }_{ 3 } \end{matrix} \right) \times \left( \begin{matrix} { \textbf{w} }_{ 1 } \\ { \textbf{w} }_{ 2 } \\ { \textbf{w} }_{ 3 } \end{matrix} \right) =\left( \begin{matrix} { \textbf{v} }_{ 2 }{ \textbf{w} }_{ 3 }-{ \textbf{v} }_{ 3 }{ \textbf{w} }_{ 2 } \\ { \textbf{v} }_{ 3 }{ \textbf{w} }_{ 1 }-{ \textbf{v} }_{ 1 }{ \textbf{w} }_{ 3 } \\ { \textbf{v} }_{ 1 }{ \textbf{w} }_{ 2 }-{ \textbf{v} }_{ 2 }{ \textbf{w} }_{ 1 } \end{matrix} \right)\)
\(\textbf{v}\times \textbf{w}=\left| \textbf{v} \right| \left| \textbf{w} \right| \sin\theta \ \textbf{n}\)
where \(\theta\) is the angle between v w n
On this page, you should learn about
the vector product (or cross product) of two vectors properties of the vector product the magnitude of the vector product to find the area of a parallelogram The following videos will help you understand all the concepts from this page
In the following video we see how to work out the vector product using the formula, what this means and how to use the right-hand rule to find its direction.
Properties of Vector Product
There are 4 important properties of the vector product that you will need to learn. These properties are often used in proofs.
\(\textbf{v}\times\textbf{w} =-\textbf{w} \times \textbf{v}\\ \textbf{u} \times (\textbf{v}+\textbf{w} )= \textbf{u} \times \textbf{v}+\textbf{u} \times \textbf{w} \\ (k\textbf{v})\times \textbf{w} =k(\textbf{v}\times \textbf{w})\\ \textbf{v}\times \textbf{v}=0 \)
Show that \((\textbf{v}+\textbf{w})\times (\textbf{v}-\textbf{w})=2\textbf{w}\times \textbf{v}\)
Magnitude of Vector Product
We know that \(\textbf{v}\times \textbf{w}= \color{red} {\left| \textbf{v} \right| \left| \textbf{w} \right| sin\theta} \ \textbf{n}\)
where \(\theta\) is the angle between v w n unit normal vector.
Hence if we find the magnitude of the vector product
\(\color{red} {\left|\textbf{v}\times \textbf{w}\right|} = \color{red} {\left| \textbf{v} \right| \left| \textbf{w} \right| sin\theta} \)
If we divide this by two, we get something familiar
\(\frac {1}{2} {\left|\textbf{v}\times \textbf{w}\right|} = \frac {1}{2} {\left| \textbf{v} \right| \left| \textbf{w} \right| sin\theta} \)
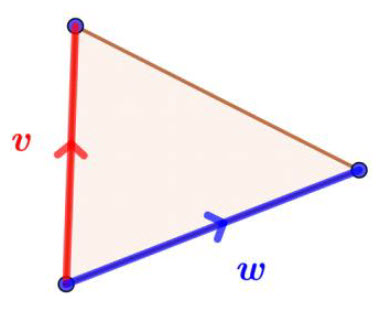
You may recall that formula for the area of a triangle is \(A = \frac {1}{2}absin \theta\)
Hence...
Area of a triangle = \(\frac {1}{2} {\left|\textbf{v}\times \textbf{w}\right|}\)
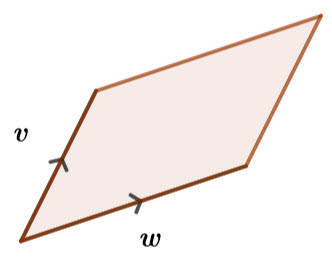
It therefore follows that for a paralellogram...
Area of a parallelogram = \(\left| \textbf{v}\times \textbf{w} \right| \)
In the following video, we are going to look at this application of the vector product. In this example we use the vector product to find the area of a parallelogram:
A parallelogram has two adjacent sides formed by the vectors 2i - j + 3k and ai + 4k . The area of the parallelogram is \(\sqrt{26}\) . Find the possible values of a.
Vector and Scalar Product
Here is an example that combines the vector product and the scalar product
Prove that \({ \left| \textbf{v}\times \textbf{w} \right| }^{ 2 }={ \left| \textbf{v} \right| }^{ 2 }{ \left| \textbf{w} \right| }^{ 2 }-{ (\textbf{v}\cdot \textbf{w}) }^{ 2 }\)
Here is a quiz that practises the skills from this page
Find a
\(\left( \begin{matrix} 1 \\ 2 \\ 0 \end{matrix} \right) \times \left( \begin{matrix} 0 \\ -1 \\ 2 \end{matrix} \right) =\left( \begin{matrix} 4 \\ -2 \\ a \end{matrix} \right) \)
\(\textbf{v}\times \textbf{w}=\left( \begin{matrix} { \textbf{v} }_{ 1 } \\ { \textbf{v} }_{ 2 } \\ { \textbf{v} }_{ 3 } \end{matrix} \right) \times \left( \begin{matrix} { \textbf{w} }_{ 1 } \\ { \textbf{w} }_{ 2 } \\ { \textbf{w} }_{ 3 } \end{matrix} \right) =\left( \begin{matrix} { \textbf{v} }_{ 2 }{ \textbf{w} }_{ 3 }-{ \textbf{v} }_{ 3 }{ \textbf{w} }_{ 2 } \\ { \textbf{v} }_{ 3 }{ \textbf{w} }_{ 1 }-{ \textbf{v} }_{ 1 }{ \textbf{w} }_{ 3 } \\ { \textbf{v} }_{ 1 }{ \textbf{w} }_{ 2 }-{ \textbf{v} }_{ 2 }{ \textbf{w} }_{ 1 } \end{matrix} \right)\)
Find b
\(\left( \begin{matrix} 2 \\ -2 \\ 1 \end{matrix} \right) \times \left( \begin{matrix} 1 \\ 2 \\ 0 \end{matrix} \right) =\left( \begin{matrix} -2 \\ b \\ 6 \end{matrix} \right) \)
\(\textbf{v}\times \textbf{w}=\left( \begin{matrix} { \textbf{v} }_{ 1 } \\ { \textbf{v} }_{ 2 } \\ { \textbf{v} }_{ 3 } \end{matrix} \right) \times \left( \begin{matrix} { \textbf{w} }_{ 1 } \\ { \textbf{w} }_{ 2 } \\ { \textbf{w} }_{ 3 } \end{matrix} \right) =\left( \begin{matrix} { \textbf{v} }_{ 2 }{ \textbf{w} }_{ 3 }-{ \textbf{v} }_{ 3 }{ \textbf{w} }_{ 2 } \\ { \textbf{v} }_{ 3 }{ \textbf{w} }_{ 1 }-{ \textbf{v} }_{ 1 }{ \textbf{w} }_{ 3 } \\ { \textbf{v} }_{ 1 }{ \textbf{w} }_{ 2 }-{ \textbf{v} }_{ 2 }{ \textbf{w} }_{ 1 } \end{matrix} \right)\)
The vector product of two parallel vectors = 0
\(i\times j\quad =\)
Use the right hand rule: first finger pointing in x direction, second finger pointing in y direction.
Your thumb should be pointing along the z axis.
\(k\times j=\)
\(\textbf{v}\times\textbf{w} =-\textbf{w} \times \textbf{v}\)
\(i\times k=\)
Use the right hand rule: first finger pointing in x direction, second finger pointing in z direction.
Your thumb should be pointing along the negative y direction.
Find all the vectors which are perpendicular to \(a\times b\)
\(a\times b\) is a vector perpendicular to a b
Which of the following is equal to \(\left| \textbf{v}\times \textbf{w}\right|\)
\((a-b)\times (a+b)=\quad \)
\((a-b)\times (a+b)=a\times a+a\times b-b\times a-b\times b\\=0 +a\times b+a\times b+0\\=2a\times b \)
\(a\times b\) is perpendicular to a.
The scalar product of two perpendicular vector = 0
a \(\left( \begin{matrix} 2 \\ 3 \\ -5 \end{matrix} \right) \) and b \(\left( \begin{matrix} 3 \\ -2 \\ 4 \end{matrix} \right) \)
Find \(\textbf{a}\times \textbf{b}\)
\(\textbf{v}\times \textbf{w}=\left( \begin{matrix} { \textbf{v} }_{ 1 } \\ { \textbf{v} }_{ 2 } \\ { \textbf{v} }_{ 3 } \end{matrix} \right) \times \left( \begin{matrix} { \textbf{w} }_{ 1 } \\ { \textbf{w} }_{ 2 } \\ { \textbf{w} }_{ 3 } \end{matrix} \right) =\left( \begin{matrix} { \textbf{v} }_{ 2 }{ \textbf{w} }_{ 3 }-{ \textbf{v} }_{ 3 }{ \textbf{w} }_{ 2 } \\ { \textbf{v} }_{ 3 }{ \textbf{w} }_{ 1 }-{ \textbf{v} }_{ 1 }{ \textbf{w} }_{ 3 } \\ { \textbf{v} }_{ 1 }{ \textbf{w} }_{ 2 }-{ \textbf{v} }_{ 2 }{ \textbf{w} }_{ 1 } \end{matrix} \right)\)
a b a b \((\textbf{a}\times \textbf{b})\cdot \textbf{a}=0\) and \((\textbf{a}\times \textbf{b})\cdot \textbf{b}=0\)
a i j k b i j k
Find a unit vector that is perpendicular to a b
Use the vector product
\(\textbf{v}\times \textbf{w}=\left( \begin{matrix} { \textbf{v} }_{ 1 } \\ { \textbf{v} }_{ 2 } \\ { \textbf{v} }_{ 3 } \end{matrix} \right) \times \left( \begin{matrix} { \textbf{w} }_{ 1 } \\ { \textbf{w} }_{ 2 } \\ { \textbf{w} }_{ 3 } \end{matrix} \right) =\left( \begin{matrix} { \textbf{v} }_{ 2 }{ \textbf{w} }_{ 3 }-{ \textbf{v} }_{ 3 }{ \textbf{w} }_{ 2 } \\ { \textbf{v} }_{ 3 }{ \textbf{w} }_{ 1 }-{ \textbf{v} }_{ 1 }{ \textbf{w} }_{ 3 } \\ { \textbf{v} }_{ 1 }{ \textbf{w} }_{ 2 }-{ \textbf{v} }_{ 2 }{ \textbf{w} }_{ 1 } \end{matrix} \right)\)
A unit vector is a vector with magnitude = 1
a b a b \((\textbf{a}\times \textbf{b})\cdot \textbf{a}=0\) and \((\textbf{a}\times \textbf{b})\cdot \textbf{b}=0\)
The area of a parallelogram formed by two adjacent vectors a b
a \(\left( \begin{matrix} -3 \\ 4 \\ k \end{matrix} \right) \) b \(\left( \begin{matrix} 3 \\ -2 \\ -2 \end{matrix} \right) \)
Find k
Area of parallelogram = \(\left| \textbf{a}\times \textbf{b} \right| \)
Given that \(\textbf{u}\times \textbf{v} = \textbf{u}\times \textbf{w}\) show that \(\textbf{v}- \textbf{w} \) is parallel to \(\textbf{u}\)
If \(\textbf{a}\times \textbf{b}=0\) a b
\(\textbf{u}\times \textbf{v} = \textbf{u}\times \textbf{w}\)
\(\textbf{u}\times \textbf{v} - \textbf{u}\times \textbf{w}=0\)
\(\textbf{u}\times ( \textbf{v} - \textbf{w})=0\)
Since the vector product is zero, the vectors are parallel
a) For any two vectors v w
\({ \left| \textbf{v}\times \textbf{w} \right| }^{ 2 }+{ \left( \textbf{v}\cdot \textbf{w} \right) }^{ 2 }={ \left| \textbf{v} \right| }^{ 2 }{ \left| \textbf{w} \right| }^{ 2 }\)
b) Hence , find \(\textbf{v}\cdot \textbf{w}\) if
\({ \left| \textbf{v} \right| }=3\)
\({ \left| \textbf{w} \right| }=4\)
\(\textbf{v}\times \textbf{w} =\left( \begin{matrix} -1 \\ 2 \\ 3 \end{matrix} \right) \)
Look in formula booklet for formulae for \({ \left| \textbf{v}\times \textbf{w} \right| }\) and \(\textbf{v}\cdot \textbf{w}\)
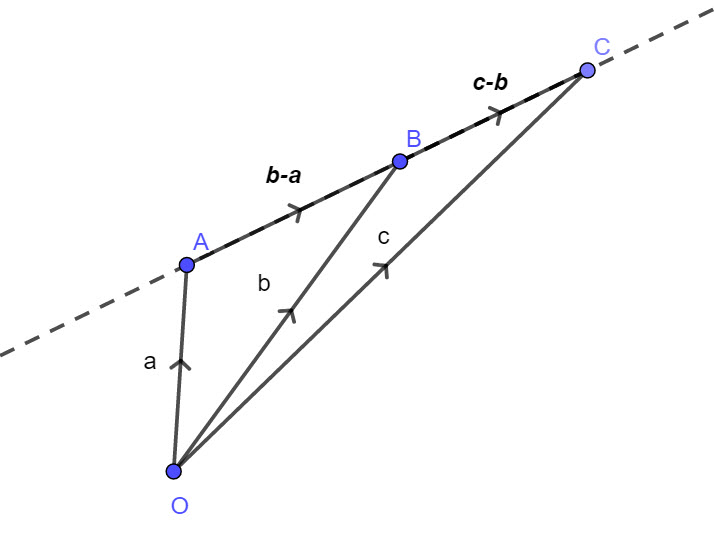
The points A, B and C are given by the position vectors a b c
If A, B and C are collinear, show that
\(\textbf{b}\times \textbf{c}=\textbf{a}\times (\textbf{c}-\textbf{b})\)
If A, B and C are collinear, then \(\overrightarrow { AB } \) \(\overrightarrow { BC } \)
What do you know about the vector product of parallel vectors?
a b
Show that \(|\textbf{a}×\textbf{b}|^{ 2 }+|\textbf{a} ∙\textbf{b}|^{ 2 }=(\textbf{a}\textbf{b})^{ 2 }\)
\(|\textbf{a}×\textbf{b}|=\textbf{a}\textbf{b}sin\theta \) MY PROGRESS
Self-assessment How much of Vector Product have you understood?
My notes
Which of the following best describes your feedback?







 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn