 In this page, we will look at another measure of angles, that is, radians. This is a far more useful measure than degrees. Formula for calculating arcs and sectors become simpler and most importantly, we need to use radian measure whenever we are doing Calculus with trigonometric functions. Calculating arc lengths and sector areas is straightforward, but take care, some of the questions on this topic can be challenging. Make sure that you try some of the more difficult exam-style questions.
In this page, we will look at another measure of angles, that is, radians. This is a far more useful measure than degrees. Formula for calculating arcs and sectors become simpler and most importantly, we need to use radian measure whenever we are doing Calculus with trigonometric functions. Calculating arc lengths and sector areas is straightforward, but take care, some of the questions on this topic can be challenging. Make sure that you try some of the more difficult exam-style questions.
On this page, you should learn about
- radian measure for angles
- lengths of arcs
- areas of sectors
- areas of segments
Here is a quiz that practises converting degrees and radians
START QUIZ!
Radians 1 1/1
Convert \(\large\frac{\pi}{4}\)radians into degrees
\(\large \pi\) radians = 180°
Convert \(\large\frac{\pi}{6}\)radians into degrees
\(\large \pi\) radians = 180°
Convert \(\large\frac{\pi}{5}\)radians into degrees
\(\large \pi\) radians = 180°
Convert \(\large\frac{2\pi}{3}\)radians into degrees
\(\large \pi\) radians = 180°
Convert \(\large\frac{7\pi}{4}\)radians into degrees
\(\large \pi\) radians = 180°
90° = \(\large \frac{\pi}{a}\)radians
What is the value of a
a =
180° = \(\large \pi\) radians
22.5° = \(\large \frac{\pi}{a}\)radians
What is the value of a
a =
180° = \(\large \pi\) radians
20° = \(\large \frac{\pi}{a}\)radians
What is the value of a
a =
180° = \(\large \pi\) radians
72° = \(\large \frac{a}{b}\pi\) radians, where \(\large \frac{a}{b}\) is a fraction in its simplest form
What are the values of a and b
a =
b =
180° = \(\large \pi\) radians
240° = \(\large \frac{a}{b}\pi\) radians, where \(\large \frac{a}{b}\) is a fraction in its simplest form
What are the values of a and b
a =
b =
180° = \(\large \pi\) radians
Here is a quiz that practises calculations with arc lengths, sector areas and segment areas
START QUIZ!
Arc length and Sectors areas 1 1/1
The following diagram shows a circle centre O and radius 5cm. A and B lie on the circumference of the circle and \(\large A\hat{O}B\) = 2 radians.
Find the length of the arc AB
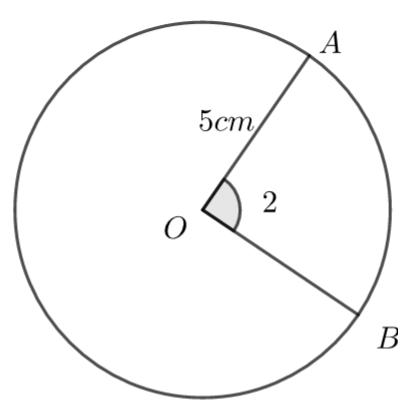
length = cm
\(\large l=r\theta=5\times 2= 10\)
The following diagram shows a circle centre O and radius 5cm. A and B lie on the circumference of the circle and \(\large A\hat{O}B\) = 2 radians.
Find the area of the sector OAB

area = cm²
\(\large A=\frac{1}{2}r^2\theta=\frac{1}{2}\times5^2\times 2=25\)
The following diagram shows a circle centre O and radius 10cm. A and B lie on the circumference of the circle and \(\large A\hat{O}B\) = 80°.
The area of the sector OAB = \(\large \frac{a\pi}{9}\)cm²
Find the value of a
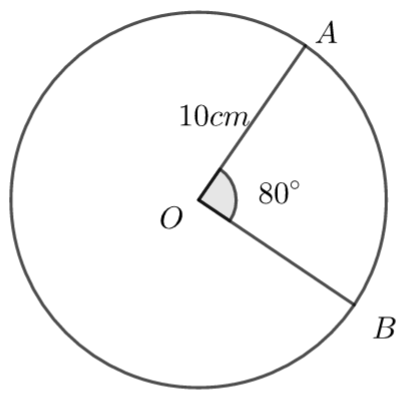
a =
\(\large A=\frac{\theta}{360}\pi r^2=\frac{80}{360}\pi \times10^2=\frac{200\pi}{9}\)
The following diagram shows a circle centre O and radius 10cm. A and B lie on the circumference of the circle and \(\large A\hat{O}B\) = 80°
The length of the arc AB =\(\large \frac{a\pi}{9}\)cm
Find the value of a

a =
\(\large l=\frac{\theta}{360}\times2\pi r=\frac{80}{360}\times2\pi \times10=\frac{40}{9}\pi\)
The following diagram shows a circle centre O and radius 4cm. A and B lie on the circumference of the circle and \(\large A\hat{O}B\) = 1 radian.
Find the area of the shaded region
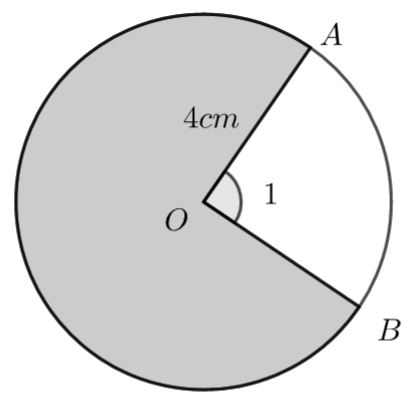
The angle subtended at the centre of the circle is \(\large 2\pi -1\)
\(\large A=\frac{1}{2}r^2\theta=\frac{1}{2}\times4^2\times (2\pi-1)=8 (2\pi-1)\)
The following diagram shows a circle centre O and radius r. A and B lie on the circumference of the circle and \(\large A\hat{O}B\) = 60°.
The length of the arc is \(\large 4\pi\) cm.
Find the radius, r
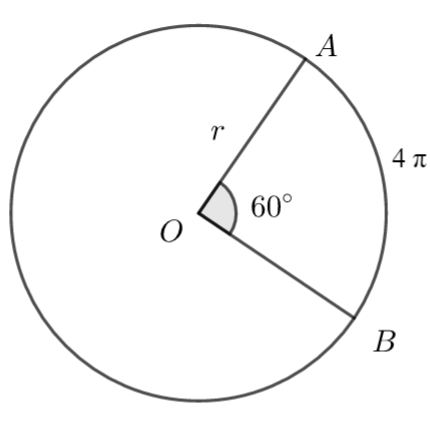
r =
\(\large l=\frac{\theta}{360}\times 2\pi r\\ \large 4\pi=\frac{60}{360}\times 2\pi r\\ \large r=12\)
The following diagram shows a circle centre O and radius r. A and B lie on the circumference of the circle and \(\large A\hat{O}B=\theta\) radians.
The length of the arc AB = r.
Find \(\large \theta\)
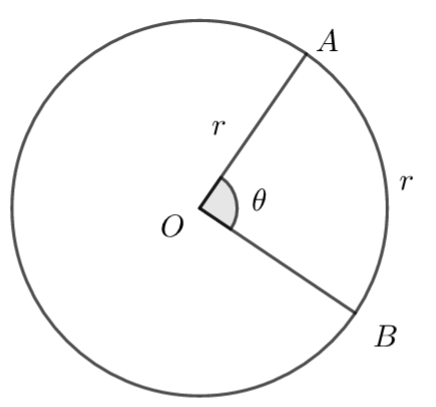
\(\large \theta\) =
This is the definition of 1 radian.
The following diagram shows a circle centre O and radius 8cm. A and B lie on the circumference of the circle and \(\large A\hat{O}B=\theta\) radians.
The area of the sector OAB is 48cm².
Find the value of \(\large \theta\)
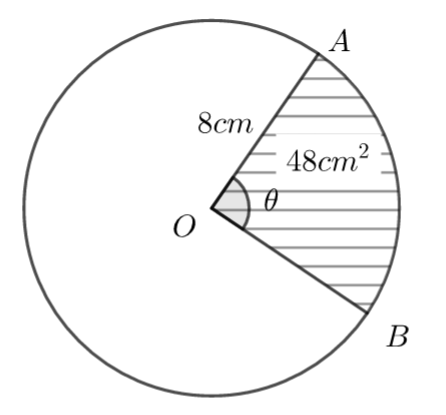
\(\large \theta\) =
\(\large A=\frac{1}{2}r^2\theta\\ \large 48=\frac{1}{2}\times 8^2\times\theta\\ \large \theta = \frac{48}{36}=1.5\)
The following diagram shows a circle centre O and radius 10cm. A and B lie on the circumference of the circle and \(\large A\hat{O}B=90°\)
Find the shaded area
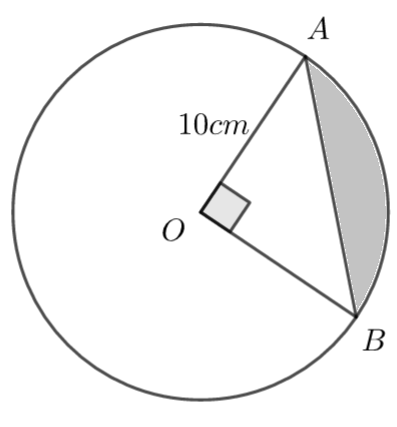
Area of segment = area of sector - area of triangle
\(\large A=\frac{\pi \times10^2}{4}-\frac{10\times10}{2}\\ \large A=25\pi-50\)
The following diagram shows a circle centre O and radius r. A and B lie on the circumference of the circle and \(\large A\hat{O}B=\theta\) radians.
Find the shaded area
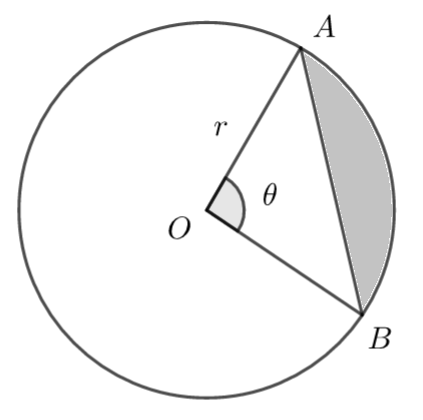
Area of segment = area of sector - area of triangle
\(\large A= \frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta\)
text



The following diagram shows a circle with centre O and radius 12cm. A and B lie on the circumference of the circle and \(\large AÔB=50°\)
a) Find the area of the minor sector OAB
b) Find the area of the triangle AOB
c) Hence, find the area of the shaded segment
Hint
Full Solution
a) The angle is given in degrees
\(\large A_{sector}= \frac{\theta}{360}\pi r^2\\ \large A_{sector}= \frac{50}{360}\pi \times 12^2\\ \large A_{sector}=20\pi\\ \large A_{sector}\approx62.831...\\ \large A_{sector}\approx62.8cm^2 \)
b) The area of the triangle is
\(\large A_{triangle}= \frac{1}{2} ab \sin C\\ \large A_{triangle}= \frac{1}{2} r^2 \sin \theta\\ \large A_{triangle}= \frac{1}{2} \times12^2 \times\sin 50°\\ \large A_{triangle}\approx55.155...\\ \large A_{triangle}\approx55.2cm^2 \)
c) The area of the segment = area of sector - area of triangle
Be careful to use a higher degree of accuracy for parts a) and b) to give the final answer correct to 3 s.f.
\(\large A_{sector}\approx62.831...-55.155...\\ \large A_{sector}\approx7.68cm^2\)



The following diagram shows a circle with centre O and radius r cm
The area of the shaded sector OAB is \(\large \frac{40\pi}{3}\) cm²
The length of the minor arc AB is \(\large \frac{10\pi}{3}\) cm
a) Find the radius of the circle
b) Find the angle \(\large \theta\) , in radians
Hint
Write an equation for the arc length and another equation for the sector area.
Full Solution
a) The area of the shaded sector OAB is \(\large \frac{40\pi}{3}\) cm²
\(\large A=\frac{1}{2}r^2\theta\\ \large \frac{40\pi}{3}=\frac{1}{2}r^2\theta\\\)
The length of the minor arc AB is \(\large \frac{10\pi}{3}\) cm
\(\large l=r\theta\\ \large \frac{10\pi}{3}=r\theta\)
Let's solve these equations by substituting for \(\large r\theta\) into the area equation
\(\large \frac{1}{2}r^2\theta=\frac{40\pi}{3}\\\)
\(\large \frac{1}{2}r\times r\theta=\frac{40\pi}{3}\\\)
\(\large \frac{1}{2}r\times \frac{10\pi}{3}=\frac{40\pi}{3}\\\)
\(\large \frac{1}{2}r=4\)
r = 8 cm
We can now find the angle by substituting this value into the length equation
\(\large \frac{10\pi}{3}=8\times\theta\\ \large \theta=\frac{10\pi}{24}\\ \large \theta=\frac{5\pi}{12}\)


The following diagram shows a circle with centre O and radius 5cm and another circle with centre P and radius r. The two circles overlap meeting at points A and B. \(\large AÔP=45°\) and \(\large A\hat{P}O=30°\)

a) Show that \(\large r=5\sqrt{2}\) cm
b) Hence, show that the shaded area bounded by the two circles is \(\large \frac{25}{12}(7\pi-6-6\sqrt3)\) cm²
Hint
a) You can use the Sine Rule to find r.
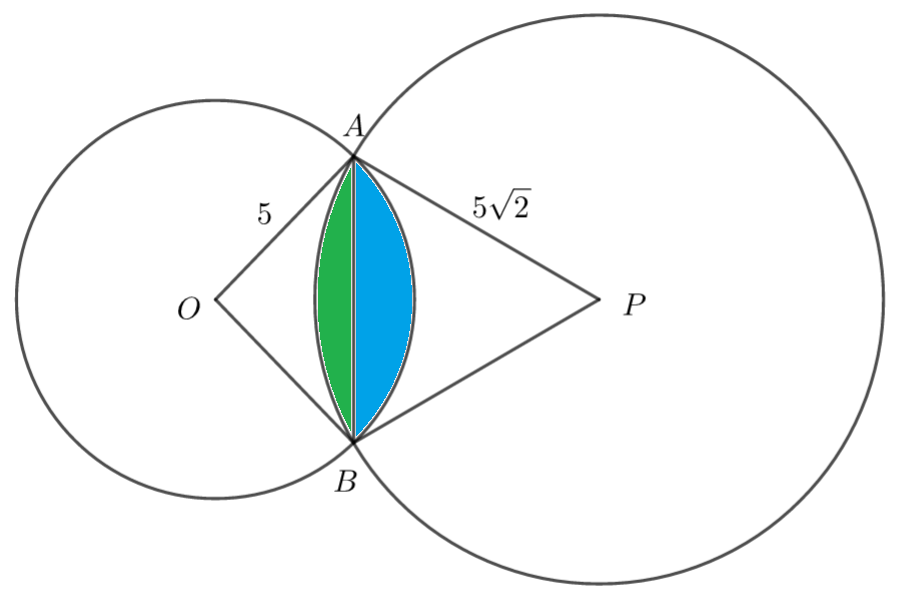
Full Solution
a)
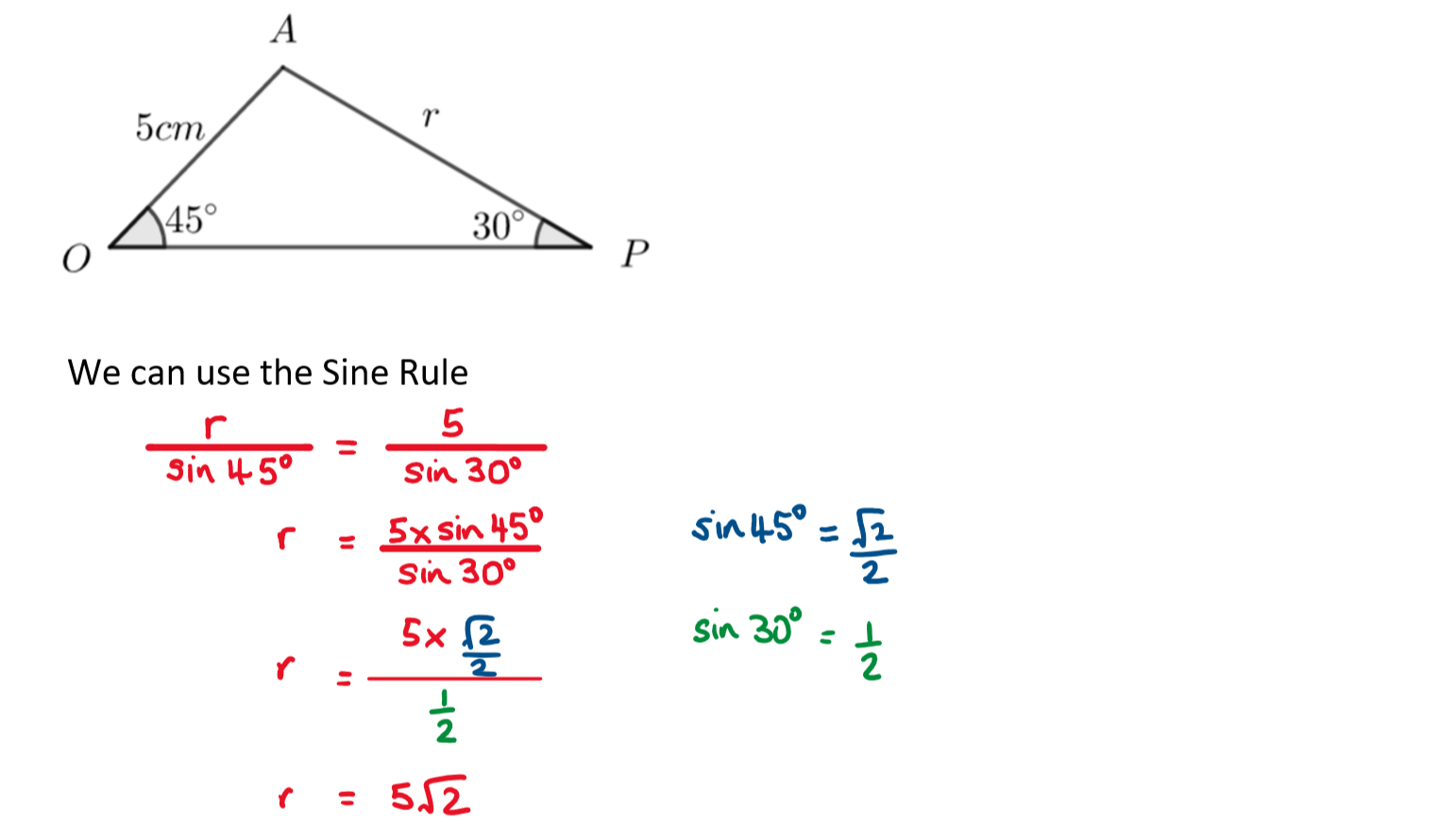
b) Divide the shaded area into two parts.


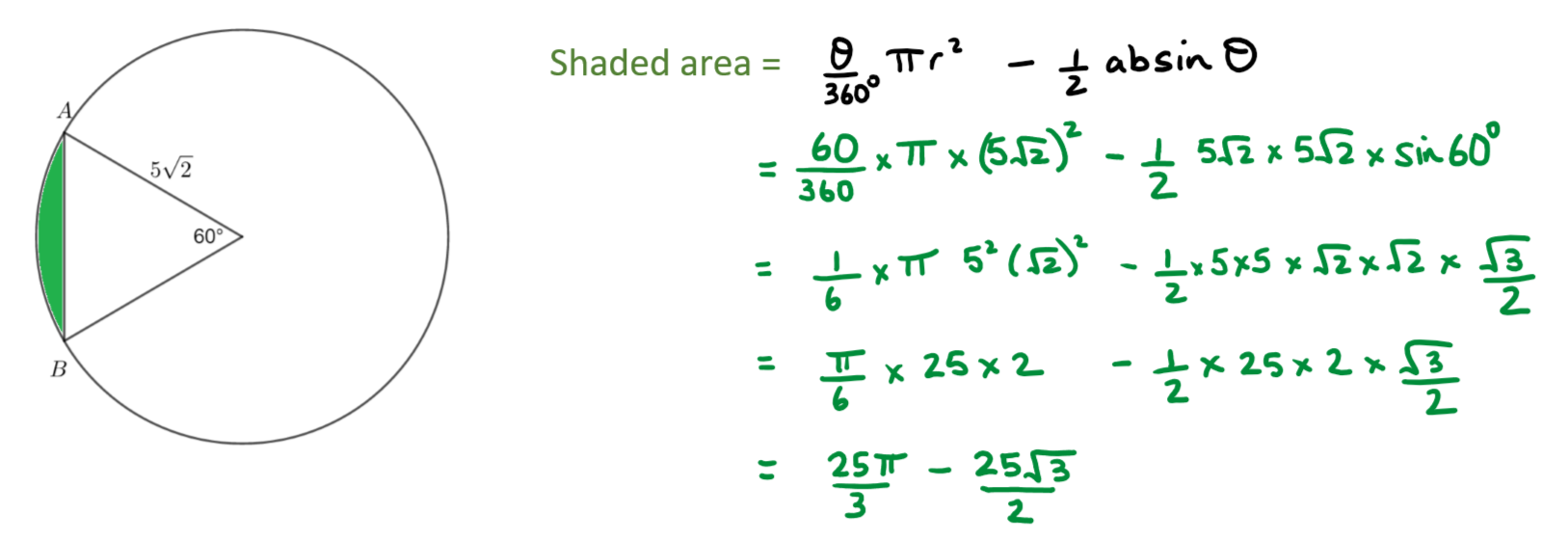



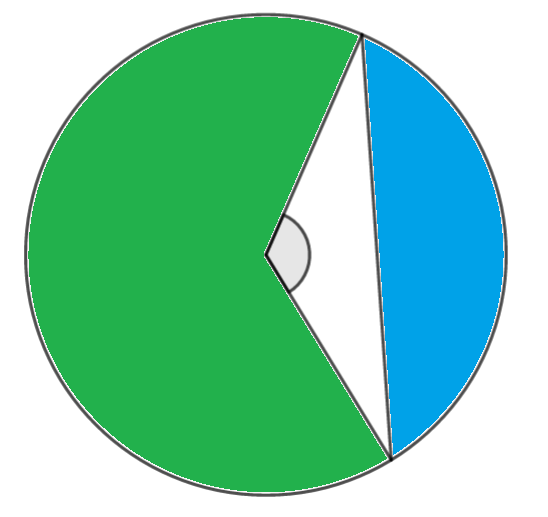
The following diagram shows a circle with centre O and radius r. A and B are points on the circumference of the circle and \(\large A\hat{O} B =\theta\) radians
The area of the green shaded region is three times greater than the area of the blue region.
a) Show that \(\large \sin \theta=\frac{4\theta-2\pi}{3}\)
b) Find the value of \(\large \theta\) , giving your answer correct to 3 significant figures.
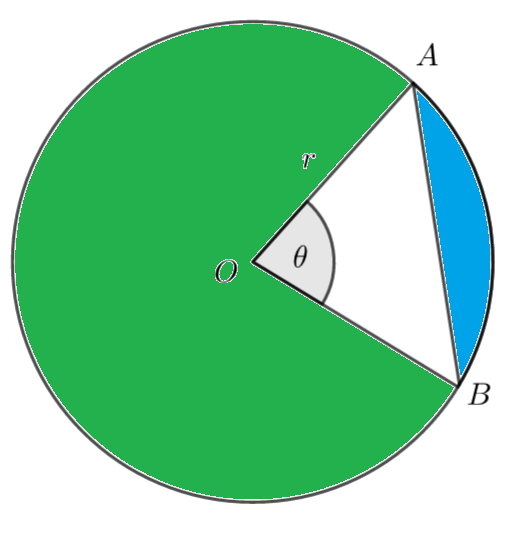
Hint
a) The area of the blue segment = area of sector - area of triangle
Full Solution
a)

area of the blue segment = area of sector - area of triangle
\(\large A_{segment}=\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta\)
 The angle subtended by the the green sector is \(\large 2\pi-\theta\)
The angle subtended by the the green sector is \(\large 2\pi-\theta\)
Area of the green sector is
\(\large A_{sector}=\frac{1}{2}r^2(2\pi-\theta)\)
The area of the green sector = three times the area of the blue segment
\(\large \frac{1}{2}r^2(2\pi-\theta)\) = 3 \(\large (\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta)\)
\(\large \frac{1}{2}r^2(2\pi-\theta)=\frac{3}{2}r^2(\theta-\sin\theta)\)
\(\large 2\pi-\theta=3(\theta-\sin\theta)\\ \large 2\pi-\theta=3\theta-3\sin\theta\\ \large 3\sin\theta=4\theta-2\pi\\ \large \sin\theta=\frac{4\theta-2\pi}{3}\)
b) We can solve this equation using our graphical equation.You can plot the graphs of \(\large y=\sin\theta\\ \) and \(\large y=\frac{4\theta-2\pi}{3}\) and find the point of intersection
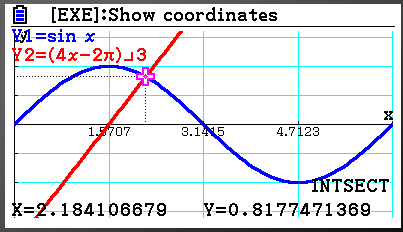
\(\large \theta \approx2.18\)
The diagram looks approaximately like the following



The following diagram shows a circle with centre O and radius r. Points A and B lie on the circumference of the circle and \(\large A\hat{O}B=\theta\) radians. The tangents to the circle A and B intersect at C.
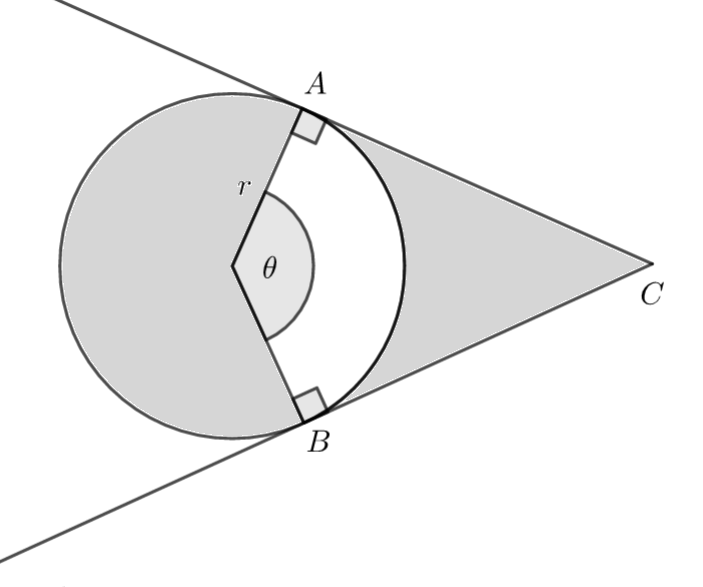
a) Show that \(\large AC=r\tan (\frac{\theta}{2})\)
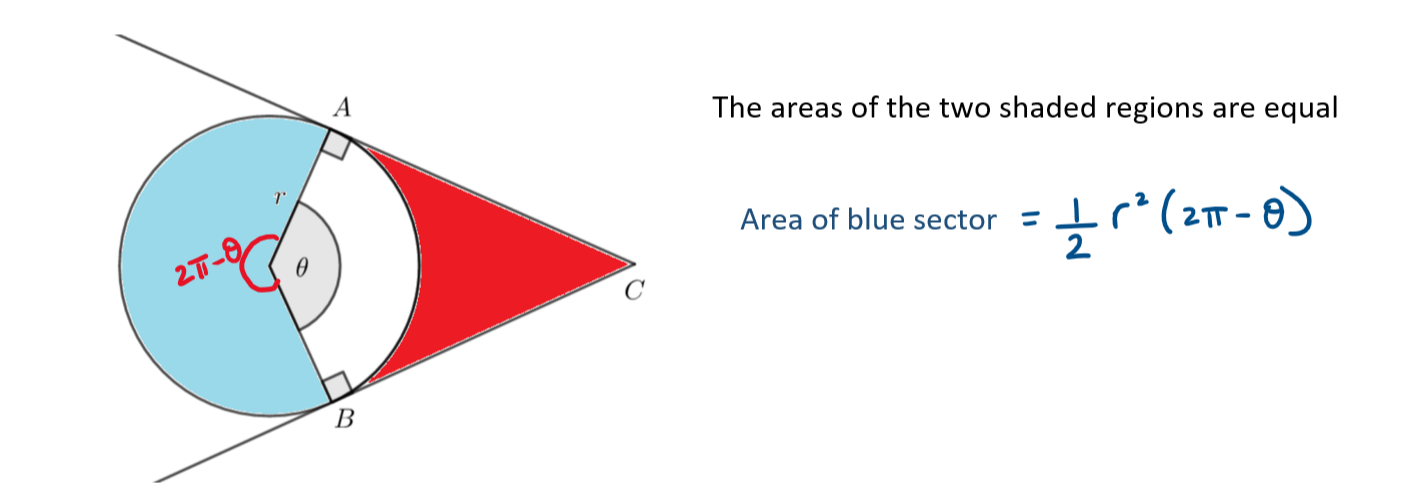
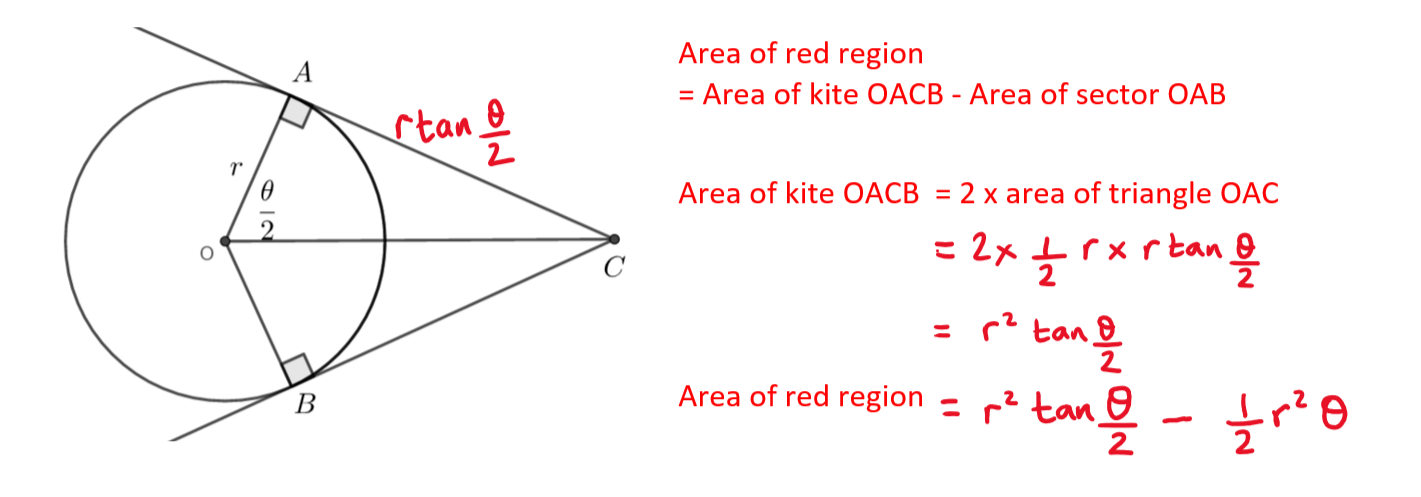
b) Hence, find the value of \(\large \theta\) when the two shaded regions have an equal area.
Hint
b) Area of red region = Area of kite OACB - Area of sector OAB
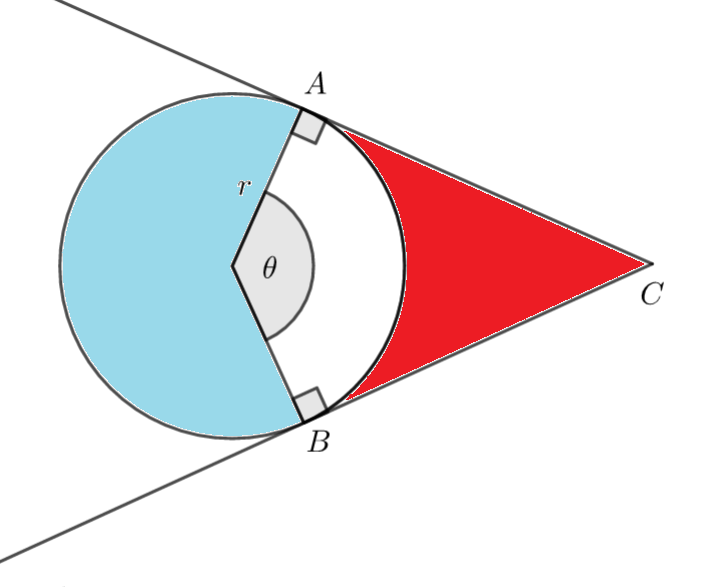
Full Solution
a) Triangle OAC is a right angled triangle, so we can use right-angled triangle trigonometry to work out the length AC (opposite to the angle \(\large\frac{\theta}{2}\)
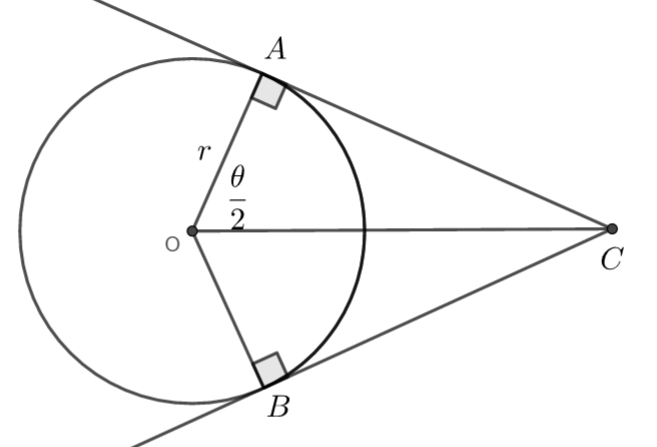
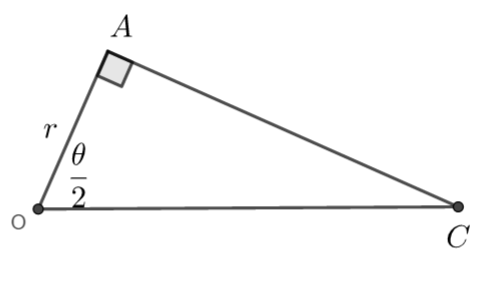
\(\large \tan\frac{\theta}{2}=\frac{AC}{r}\)
\(\large AC=r\tan\frac{\theta}{2}\)
b)

How much of Radians, Arcs and Sectors have you understood?
Feedback
Which of the following best describes your feedback?



 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn