The Unit Circle is probably the most important topic to understand from the whole of trigonometry. Lots of the properties of the trigonometric functions can be found from the unit circle. All the work on this page will help us understand all of these properties. This is essential knowledge, for example, for us to be able to solve trigonometric equations.
On this page, you should learn about
- the definition of \(\sin \theta\) and \(\cos \theta\) in terms of the unit circle
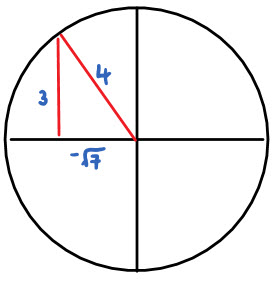
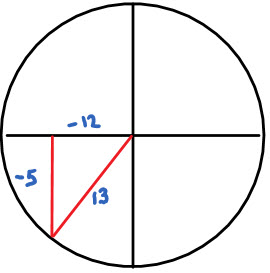
- If we consider a unit circle (a circle of radius 1), then
\(sin\theta=\frac{opposite}{hypotenuse}=\frac{opposite}{1}\)
\(cos\theta=\frac{adjacent}{hypotenuse}=\frac{adjacent}{1}\)
- the definition of \(\tan \theta\) as \(\frac{opposite}{adjacent}=\frac{\sin\theta}{\cos\theta}\)
- exact values of trigonometric ratios of 0°, 30°, 45°, 60°, 90°
- the symmetry properties of graphs of trigonometric functions
- the reciprocal trigonometric ratios \(cosec \theta\), \(sec \theta\), \(cot\theta\)
Print from here
Here is a quiz that practises the skills from this page
START QUIZ!
Drag the function next to the correct graph
sinx cos(-x) -cosx tanx -tanx -sinx sin(-x)
 | f(x) = |  | f(x) = |
 | f(x) = |  | f(x) = |
Note that cosx = cos(-x)
This question is about remembering the exact values for trigonometric ratios. Try to do it without your calculator.
Enter the correct angle. Each answer is an angle between 0 and 90°.
There is no need to enter the ° symbol
| \(\frac { 1 }{ 2 } \) = cos | \(\frac { \sqrt { 3 } }{ 2 } \) = sin | 2 = cosec |
| \(\frac { \sqrt { 2 } }{ 2 } \)= sin | \(\sqrt{3}\)= tan | 1 = cot |
| \(\sqrt{3}\)= cot | \(\sqrt{2}\) =sec | \(\frac { \sqrt { 3 } }{ 2 } \) = cos |
Drag the answers into the correct places
sin150° cos120° tan225° sin270° cos330° cos210°
| \(\frac{1}{2}\) = | 1 = | \(\frac { \sqrt { 3 } }{ 2 } \) = |
| -1 = | \(-\frac { \sqrt { 3 } }{ 2 } \) = | \(-\frac{1}{2}\) = |
Match up the following answers with their correct pair
cos150° sin330° sin120°
-sin60° =
cos120° =
cos330° =
Match up the following answers with their correct pair
sin300° tan(-60°) -tan150°
sin240° =
tan120° =
tan210° =
Match up the following answers with their correct pair
cosec135° cot315° sec225°
-sec 135° =
cot(-45°) =
cosec225° =
Given that \(tan\theta = \frac{1}{3}\) and \(\pi<\theta<\frac{3\pi}{2}\) , then
\(sin\theta\) = \(\frac{a}{\sqrt{10}}\)\(cos\theta\) = \(\frac{b}{\sqrt{10}}\)
What are the values of a and b?
a =
b =
Given that \(sin\theta = \frac{3}{4}\) and \(90°< \theta <180°\) ,
find \(cos\theta\)
Given that \(cos\theta = \frac{3}{5}\) and \(\frac{3\pi}{2}<\theta<2\pi\) , then
\(sin\theta = \frac{a}{5}\)
\(tan\theta = \frac{b}{3}\)
What are the values of a and b?
a =
b =
Given that \(tan\theta = \frac{5}{12}\) and \(\pi<\theta<\frac{3\pi}{2}\) , then
\(cosec\theta = \frac{a}{5}\)
\(sec\theta = \frac{b}{5}\)
What are the values of a, and b?
a =
b =
How much of Unit Circle HL have you understood?
Twitter 
Facebook 
LinkedIn