On this page, you should learn about
the sine rule: \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) the cosine rule: \(c^2=a^2+b^2-2ab\cos C\) the area of a triangle =\({ 1\over 2}ab\sin C\) Here is a quiz that practises the skills from this page
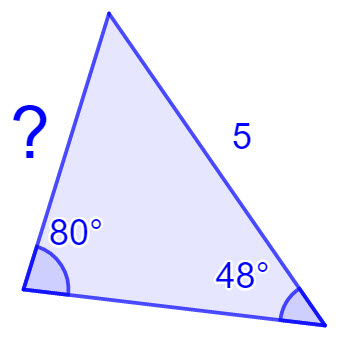
Using the following diagram, complete the following equation
\(\frac{5}{sinA°}=\frac{b}{sin57°}\)
Using the Sine Rule, a is opposite A and b is opposite B
\(\frac{a}{sinA}=\frac{b}{sinB}\)
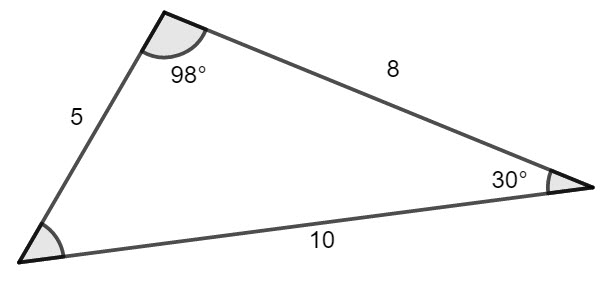
Using the following diagram, complete the following equation
\(\frac{5}{sinA°}=\frac{8}{sinB°}\)
The side with length 8 is opposite the unmarked angle. We calculate 180-30-98 = 52
In the triangle ABC, BC = 7cm , AC = 7.5 cm and \(\hat { BAC } \) = 66°
If we use the Sine Rule to calculate \(\hat { BAC } \) , one solution is 78°.
Find another possible solution
This is the ambiguous case for the Sine Rule since sin78° = sin(180°-78°)
Using the following diagram, complete the following equation
Using the Cosine Rule
c² = a² + b² - 2abcosC
The side c is opposite the angle C
Using the following diagram, complete the following equation
cos A° = \(\frac{3^2+b^2-6.2^2}{2\times3\times c}\)
cos 124° = \(\frac{3^2+4^2-6.2^2}{2\times3\times 4}\)
In the triangle ABC, AC = 4cm , BC = 6cm and angle \(\hat { B } \) = 30°
a) Work out sin \(\hat { A } \)
There are two possible answers for angle A, A1 and A2 where A1 < A2
b) Find A1 and A2 to 3 significant figures
Using the Sine Rule
\(\frac{4}{sin30°}=\frac{6}{sinA}\)
\(sinA=\frac{6\times sin30°}{4}\)
\(sinA=\frac{6\times 0.5}{4}\)
sinA = 0.75
b) Ambiguous Case
A1 = arcsin(0.75)=48.6°
A2 = 180°- 48.6°=131.4°
Rounded to 3 s.f. A2 = 131°
\(2 \sqrt{3} \) cm and \(\hat { BAC } \) = 30°.
If BC = \(a \sqrt{b} \) , work out a and b
Using Cosine Rule
BC² = 8² + (\(2 \sqrt{3} \) )² - 2x \(2 \sqrt{3} \) x 8 x cos 30°
BC² = 64 + 4x3 - 2 x \(2 \sqrt{3} \) x 8 x \(\frac{\sqrt{3}}{2}\)
BC² = 64 + 12 - 2 x 3 x 8
BC² = 28
BC = \( \sqrt{28}\)
BC = \( 2\sqrt{7}\)
\(\hat{ABC}\) = 45° and \(\hat{ACB}\) = 75°
If BC = \(a \sqrt{b} \) , work out a and b
Using the Sine Rule
\(\frac{BC}{sin60°}=\frac{12}{sin45°}\)
\(BC=\frac{12\times sin60°}{sin45°}\)
\(BC=\frac{12\times\frac { \sqrt { 3 } }{ 2 } }{\frac { 1 }{ \sqrt { 2 } } }\)
\(BC=\frac { 6\sqrt { 3 } }{ \frac { 1 }{ \sqrt { 2 } } } \)
\(BC = 6\sqrt { 3 } \times \frac { \sqrt { 2 } }{ 1 } \)
\(BC = 6\sqrt { 6 }\)
\(3{\sqrt{2}}\) cm , AC = 8 cm and \(\hat{BAC}\) = 135°
Find the area of the triangle ABC
Area = \(\frac { 1 }{ 2 } \times 8\times 3\sqrt { 2 } \times sin135°\)
= \(\frac { 1 }{ 2 } \times 8\times 3\sqrt { 2 } \times \frac { 1 }{ \sqrt { 2 } } \)
= 12
In the triangle ABC, the area = 52 cm², AB = 12cm and AC = 13 cm.
There are two possible values for angle A, A1 and A2 where A1 < A2
Find A1 and A2 to 3 significant figures
Area = 0.5 x 12 x 13 x sinA
52 = 78 x sin A
sinA = \(\frac{52}{78}\)
A = \(arcsin(\frac{52}{78})\) = 41.8°
A2 = 180° - 41.8° = 138.2°
To 3 s.f. A2 = 138°
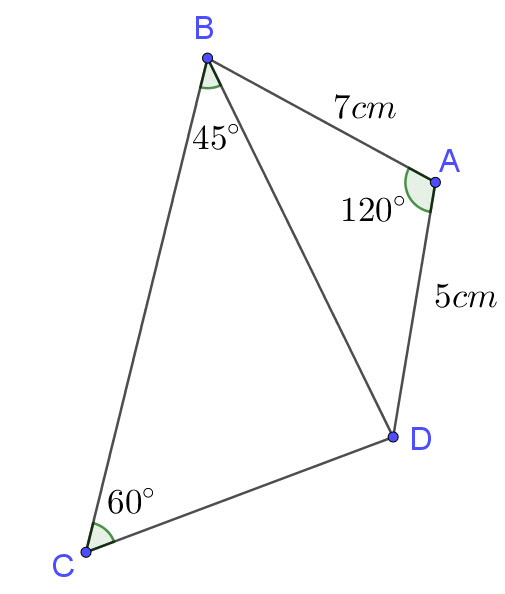
The following diagram shows a quadrilateral ABCD.
AB = 7cm , AD = 5cm ∠DAB=120° , ∠DBC=45° , ∠BCD=60°
BD = \(\sqrt{a}\)
CD = \(\sqrt{b}\)
\(a,b \in \mathbb{Z}\)
Find a b
You will need to use both the Cosine Rule and the Sine Rule in this question.
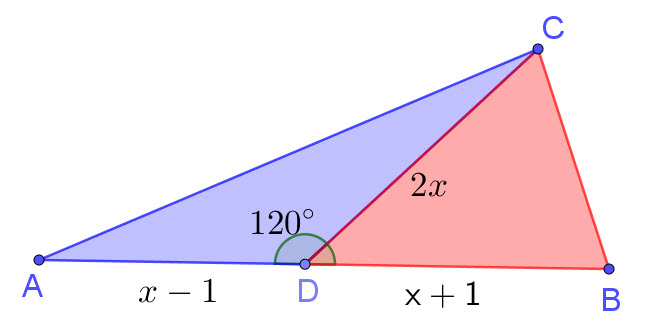
The following diagram shows a quadrilateral ABCD.
AD = x – 1 , BD = x + 1 , DC = 2x and \(\angle CDA\) = 120°
The sum of the area of triangle ADC and triangle BDC is \(4 \sqrt{3}\)
Find x
\(sin\theta = sin(180-\theta)\)
In a triangle ABC, AB = 8cm, BC = a, AC = b and \(\angle BAC\) = 30°
a) Show that \(b^2-8\sqrt{3}b+64-a^2=0\)
b) Hence find the possible values of a
a) Use the cosine rule.
The following applet might help you visualise the triangle. Drag the slider to see the different possible values that a can take
MY PROGRESS
Self-assessment How much of Sine and Cosine Rule have you understood?
My notes
Which of the following best describes your feedback?
 In this page, we will look at the Sine Rule, the Cosine Rule and the formula for the Area of a Triangle. The formula for these three are fairly straight forward to use, but don't take this topic too lightly, sometimes the exam questions can be quite challenging. Questions on this topic can even come up on the non-calculator paper when we use the angles 30°, 45°, 60°, ...
In this page, we will look at the Sine Rule, the Cosine Rule and the formula for the Area of a Triangle. The formula for these three are fairly straight forward to use, but don't take this topic too lightly, sometimes the exam questions can be quite challenging. Questions on this topic can even come up on the non-calculator paper when we use the angles 30°, 45°, 60°, ...




 In the triangle ABC, AB = 8cm, AC =
In the triangle ABC, AB = 8cm, AC = 




 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn