On this page, you should learn about
Using sine, cosine and tangent ratios to find the sides and angles of right-angled triangles. Angles of elevation and depression.. The size of an angle between between a line and a plane. Here is a quiz that practises using the three trigonometric ratios
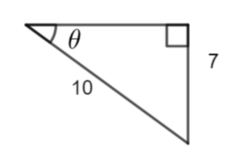
Which trigometric ratio would you use to calculate \(\large \theta\) ?
\(\large \sin\theta=\frac{opp}{hyp}\)
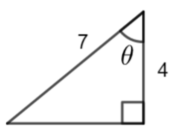
Which trigometric ratio would you use to calculate \(\large \theta\) ?
\(\large \tan\theta=\frac{opp}{adj}\)
Which trigometric ratio would you use to calculate \(\large \theta\) ?
\(\large \sin\theta=\frac{opp}{hyp}\)
Which trigometric ratio would you use to calculate \(\large \theta\) ?
\(\large \cos\theta=\frac{adj}{hyp}\)
Which trigometric ratio would you use to calculate x ?
\(\large \tan\theta=\frac{opp}{adj}\)
Which trigometric ratio would you use to calculate x ?
\(\large \cos\theta=\frac{adj}{hyp}\)
Which trigometric ratio would you use to calculate x ?
\(\large \sin\theta=\frac{opp}{hyp}\)
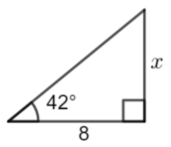
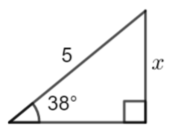
Calculate x to 3 significant figures
\(\large \sin38°=\frac{x}{5}\\
\large x=\sin38°\times5\\
\large x\approx3.08\)
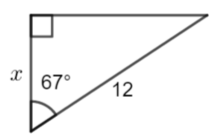
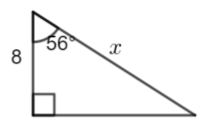
Calculate x to 3 significant figures
\(\large \cos56°=\frac{8}{x}\\
\large x=\frac{8}{\cos56°}\\
\large x\approx14.3\)
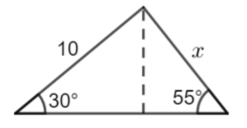
Calculate x to 3 significant figures
\(\large \sin30°=\frac{h}{10}\\
\large h=\sin30°\times10\\
\large h=5\)
\(\large \sin55°=\frac{5}{x}\\
\large x=\frac{5}{\sin55°}\\
\large x\approx6.10\)
Here is a quiz that gets you to think about trigonometry in 3 dimensions
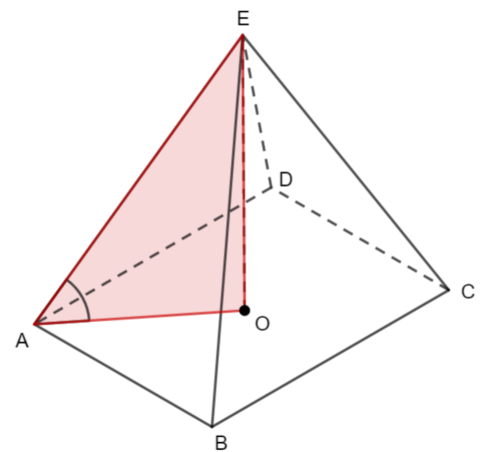
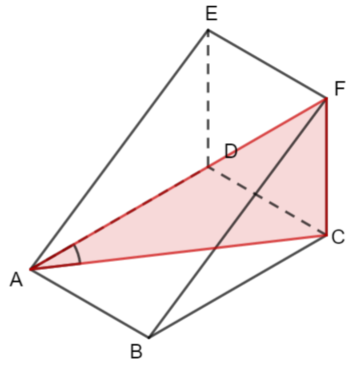
ABCDE is a rectangular-based pyramid. O is the centre of the base.
Which of the following is the angle between AE and the plane ABCD?
We can see the angle required in this diagram
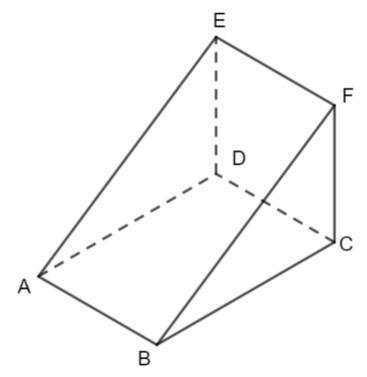
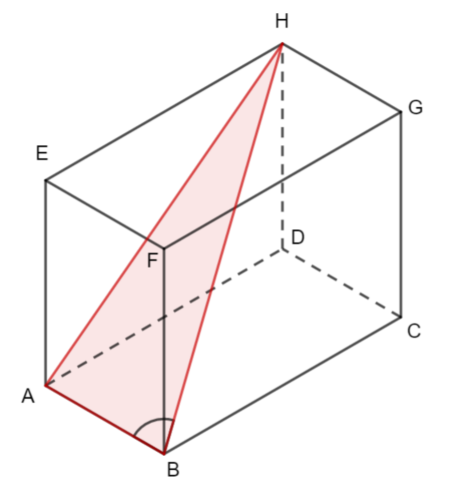
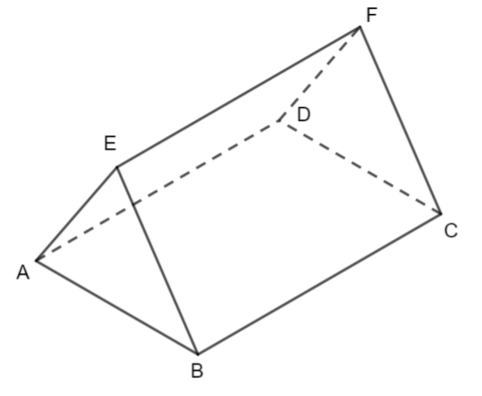
ABCDEF is a triangular prism
Which of the following is the angle between AF and the plane ABCD?
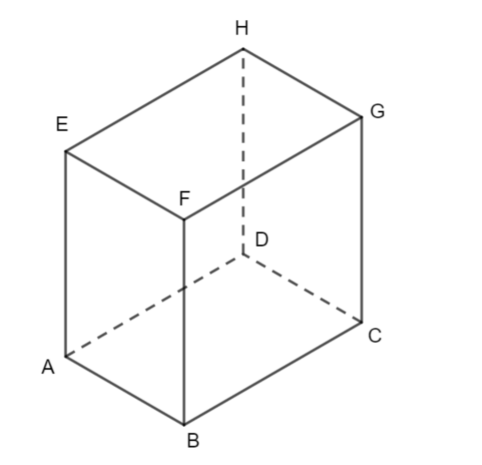
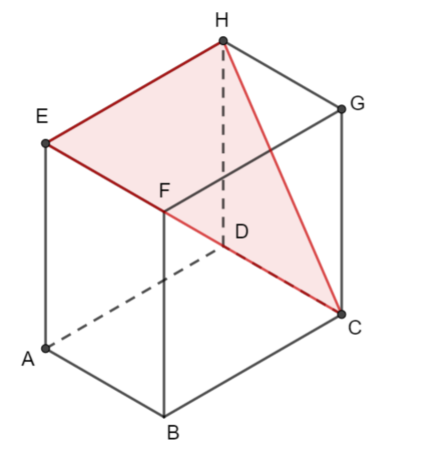
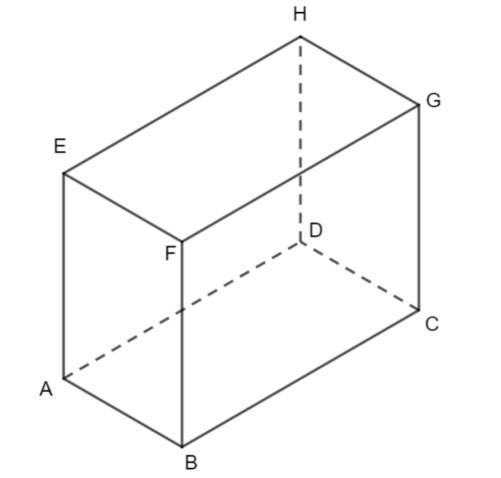
ABCDEFGH is a cuboid.
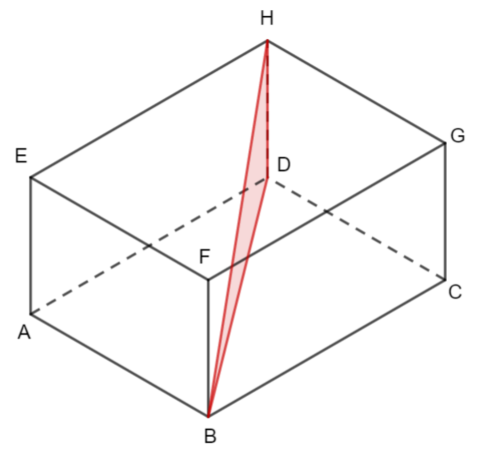
Angle HBA is the angle between HB and which plane?
Line AH lies in the plane ADHE
ABCDEFGH is a cuboid.
Which of the following is the angle between EC and the plane ABCD?
We can see the angle required in this diagram
ABCDEFGH is a cuboid.
Which of the following is the angle between EC and the plane CDHG?
We can see the angle required in this diagram
ABCDEFGH is a cuboid.
Which of the following is the angle between EC and the plane BCGF?
We can see the angle required in this diagram
ABCDEF is a triangular prism
Angle EDB is the angle between ED and which plane?
ABCDEFGH is a cuboid.
Which of the following is the angle between HB and the plane ABCD?
We can see the angle required in this diagram
ABCDEFGH is a cuboid.
Which of the following is the angle between HB and the plane ADHE?
We can see the angle required in this diagram
ABCDEFGH is a cuboid.
Which of the following is the angle between HB and the plane ABEF?
We can see the angle required in this diagram
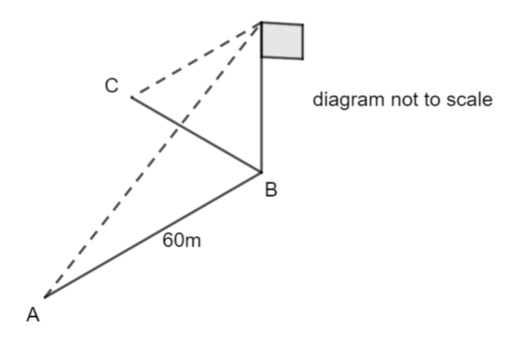
A, B and C are points on horizontal ground.
C is due West of B. A is due South of B. AB = 60m
A flagpole stands vertically at B.
From A, the angle of elevation of the top of the flagpole is 11°.
From B, the angle of elevation of the top of the flagpole is 15°.
Calculate the distance AC giving your answer to 3 significant figures.
Work out the height of the flagpole, then find length BC
\(\large\tan11°=\frac{h}{60}\\ \large h=60\times\tan11°\\ \large h\approx 11.7\)
use calculator memory to store the exact value of this length
\(\large\tan15°=\frac{h}{BC}\\ \large BC=\frac{h}{tan15°}\\ \large BC=\frac{60\times \tan11°}{tan15°}\\\\ \large BC\approx 43.5\) use the exact value of h
use calculator memory to store the exact value of this length
\(\large AC^2=AB^2+BC^2\\ \large AC^2=60^2+(43.5...)^2\\ \large AC\approx74.1m\)
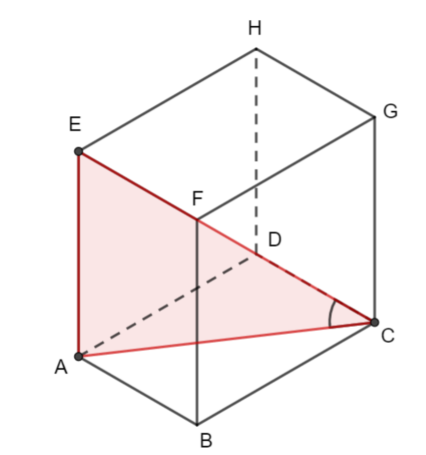
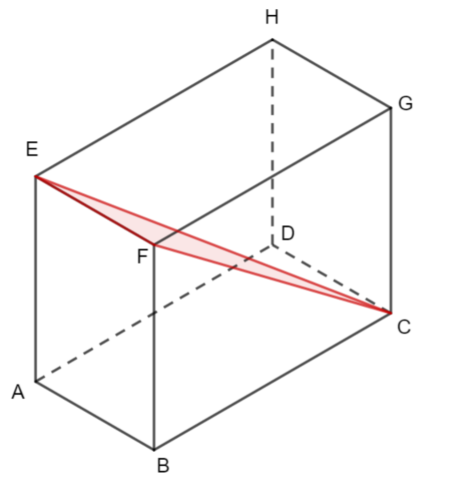
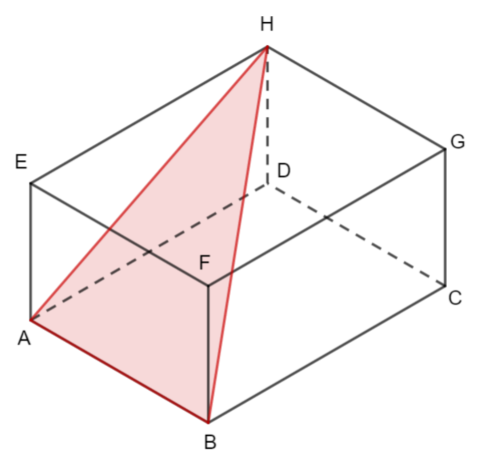
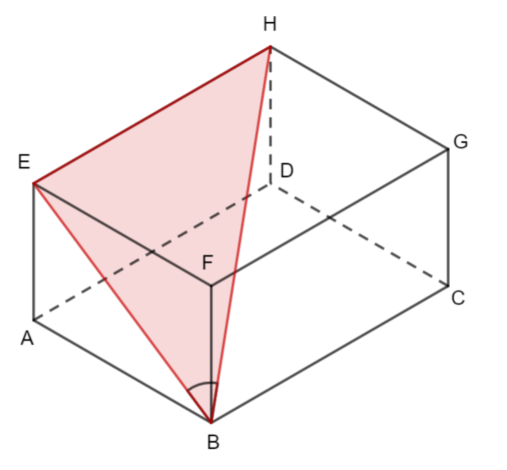
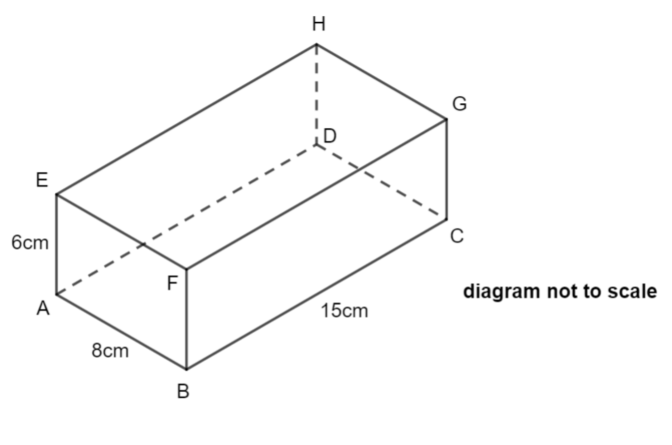
The diagram shows a cuboid ABCDEFGH. AB = 8 cm, AE = 6 cm and BC = 15 cm.
a) Find the length of AC.
Give your answer correct to 3 significant figures
b) Find the size of the angle between the line EC and the plane ABCD.
Give your answer correct to 1 decimal place.
b) Here is the right-angled triangled you should consider for this question
a)
ABC is a right-angled triangle.
Use Pythagoras' Theorem to work out AC.
AC² = 8² + 15²
AC² = 289
AC = 17cm
b)
EAC is a right-anghled triangle.
We can use trigonometry to work out the angle
\(\large \tan\theta=\frac{6}{17}\\ \large\theta=\tan^{-1}(\frac{6}{17})\\ \large\theta\approx19.4°\)
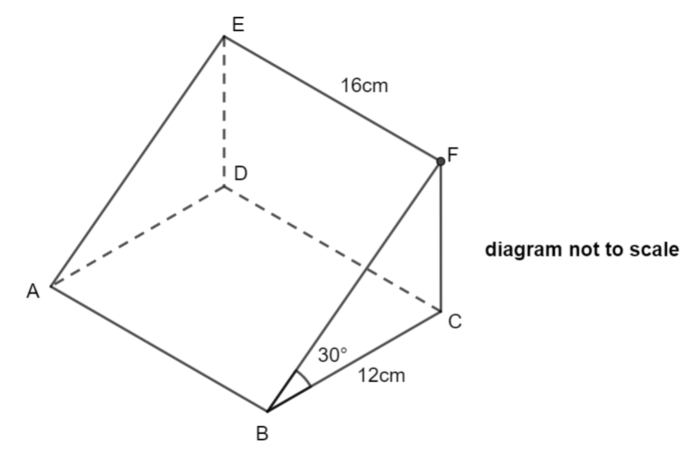
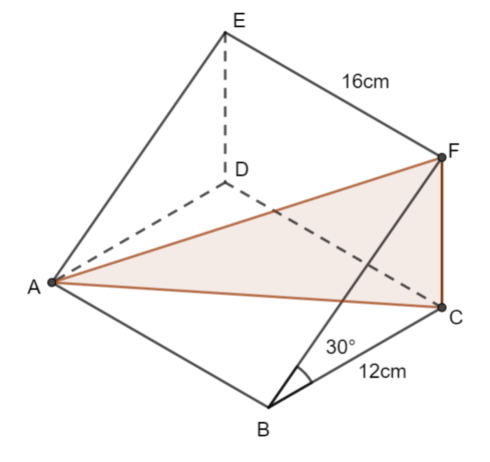
ABCDEF is a prism in which the triangle BCF is the cross section.
BC = 12cm, EF = 16cm, angle CBF = 30° and angle FCB = 90°
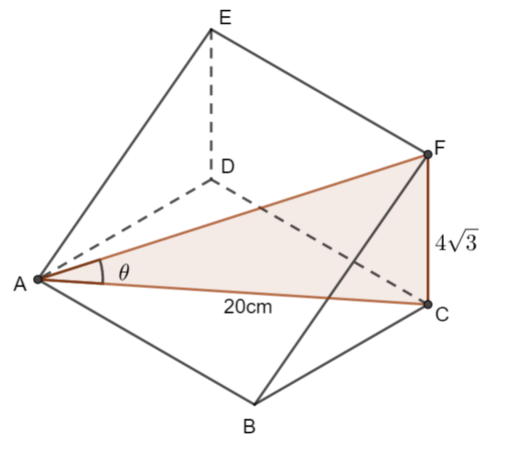
The angle AF makes with the plane ABCD is \(\large \theta\) .
Show that \(\large \tan\theta=\frac{\sqrt{3}}{5}\)
The following triangle helps you to see the angle that is required.
We can work out the lengths CF and CA
Use the triangle CBF to work out CF
\(\large \tan30°=\frac{CF}{12} \qquad \qquad \tan30°=\frac{\sqrt{3}}{3}\\ \large \frac{\sqrt{3}}{3}=\frac{CF}{12}\\ \large \frac{12\sqrt{3}}{3}=CF\\ \large CF=4\sqrt{3}\)
Use Pythagoras' Theorem to work out CA
CA² = 12² + 16²
CA² = 400
CA = 20
Now put this information in the diagram
\(\large \tan\theta=\frac{4\sqrt{3}}{20}\\ \large \tan\theta=\frac{\sqrt{3}}{5}\)
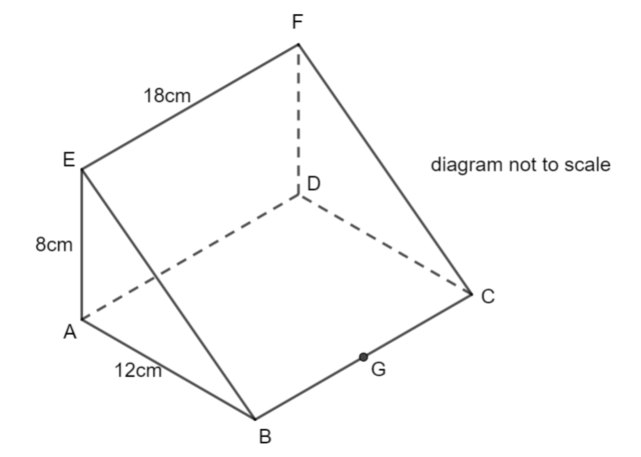
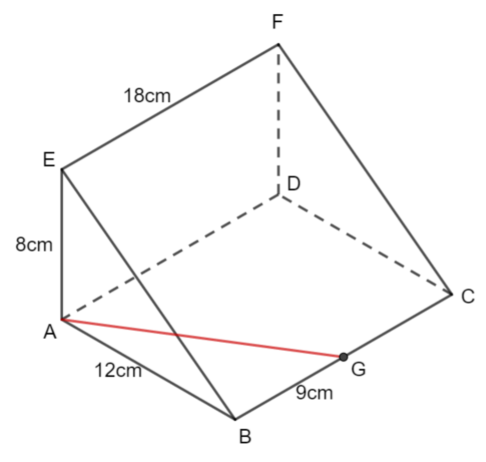
ABCDEFG is a triangular prism.
AB = 12cm, AE = 8cm, EF = 18cm.
Angle BAE = 90°
G is the midpoint of BC.
Calculate the angle between EG and the plane ABCD.
Give your answer correct to 1 decimal place.
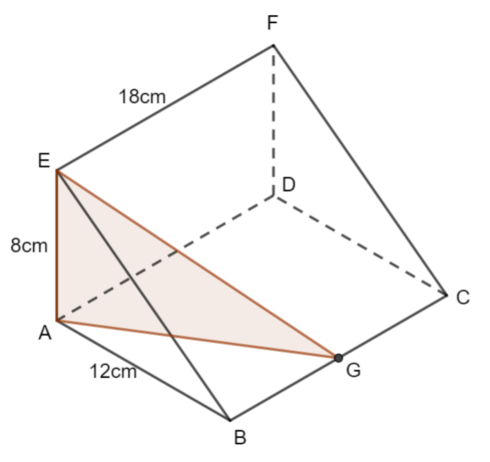
Here is the triangle that contains the angle required
G is the midpoint of BC. Therefore BG is 9cm.
AG² = 9² + 12²
AG² = 225
AG = 15
It is a right-angled triangle.
\(\large \tan\theta =\frac{8}{15}\\ \large\theta=\tan^{-1}(\frac{8}{15})\\ \large\theta\approx24.0°\)
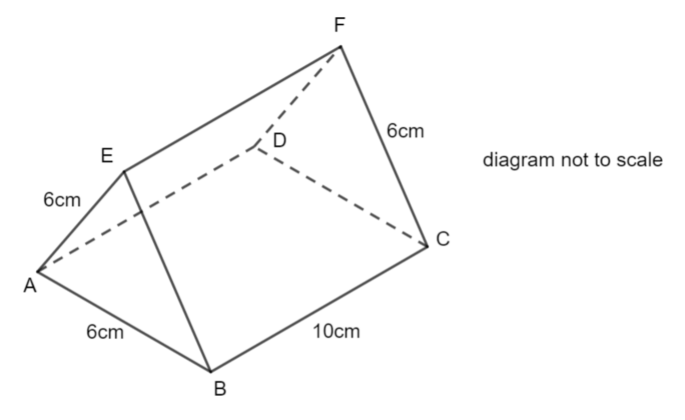
ABCDEF is a prism.
AB = AE = BE = 6cm. BC = 10cm
Calculate
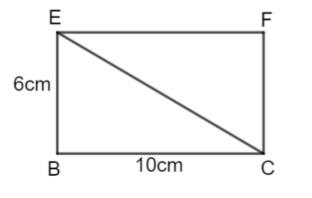
a) the length EC
b) the angle AEC
c) the angle between EC and the plane ABCD
Give lengths to 3 significant figures and angles to 1 decimal place.
For parts b) and c), the challenge is to visualise the triangles required to find the angles. The question aims to show you that the angles in part b) and c) are not the same!
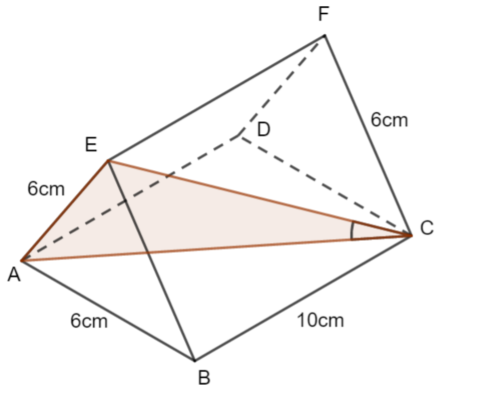
b)
c)
EC² = 10² + 6²
EC² = 136
\(\large EC = \sqrt{136}\)
We have an isoceles triangle. Use just the top half of the triangle and right-angled trigonometry to find the angle ACE (or you can use the whole triangle and the cosine rule).
\(\large \cos\theta=\frac{3}{\sqrt{136}}\\ \large \theta=\cos^{-1}(\frac{3}{\sqrt{136}})\\ \large \theta\approx75.1°\)
We know the length EC =\(\large \sqrt{136}\)
We need to find another legnth in this right-anghled triangle. Find the height of the triangle:
\(\large h^2=6^2-3^2\\ h=\sqrt{27}\)
Let \(\large \alpha\) be the angle between EC and the plane ABCD
\(\large\sin\alpha=\frac{\sqrt{27}}{\sqrt{136}}\\ \large\alpha\approx26.5°\)
MY PROGRESS
Self-assessment How much of Right-angled Trigonometry have you understood?
My notes
Which of the following best describes your feedback?
 In this page, we will learn about right-angled trigonometry. For many, this will not be a new topic, nor will it be a difficult one. However, it deserves some time, as it forms the important step to understanding most of the other work in the geometry and trigonometry topic. The challenging part is when we look at trigonometry in 3 dimensions, as it can be difficult to visualise the triangles needed. The emphasis of this page is looking at these 3-D problems.
In this page, we will learn about right-angled trigonometry. For many, this will not be a new topic, nor will it be a difficult one. However, it deserves some time, as it forms the important step to understanding most of the other work in the geometry and trigonometry topic. The challenging part is when we look at trigonometry in 3 dimensions, as it can be difficult to visualise the triangles needed. The emphasis of this page is looking at these 3-D problems.



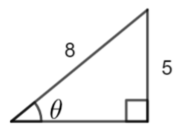
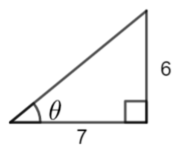
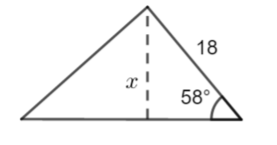
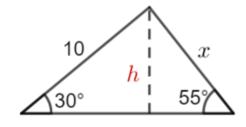 Calculate the height of the triangle first.
Calculate the height of the triangle first.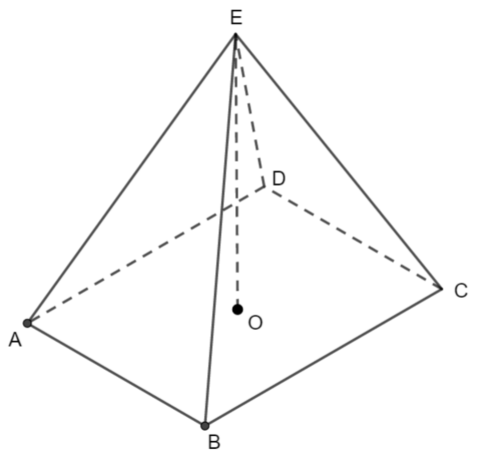

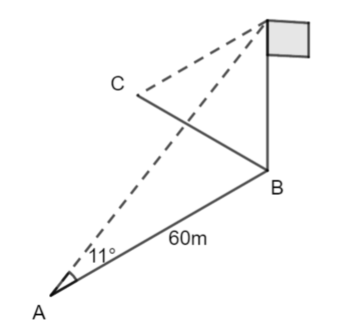 We can find the height of the flagpole
We can find the height of the flagpole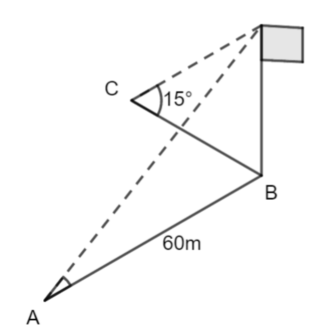 Now we can find the length BC
Now we can find the length BC
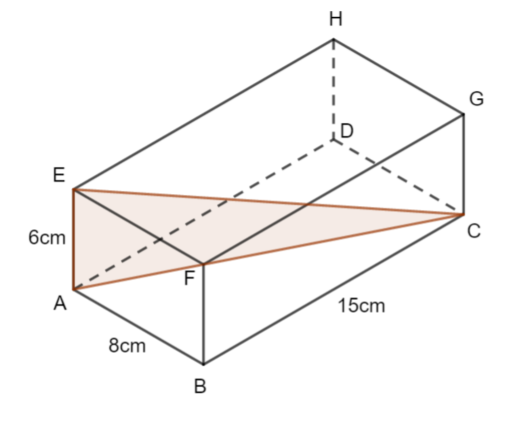
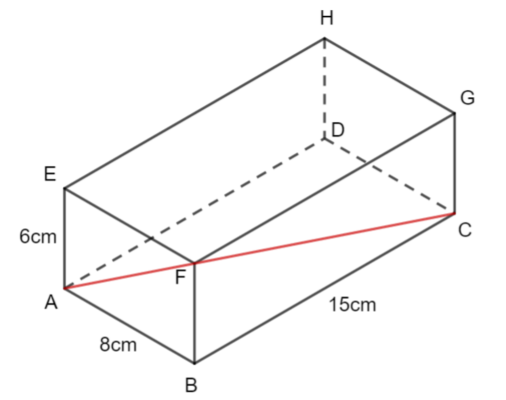
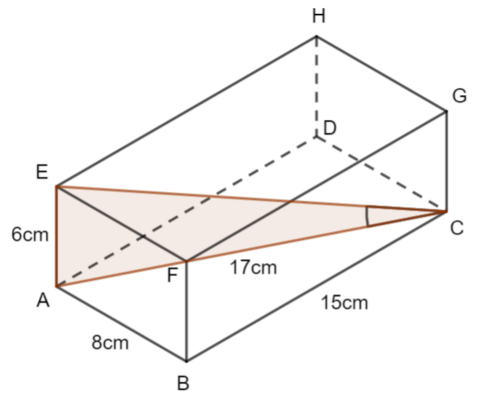 The angle between the line EC and the plane ABCD can be visualised in the diagram.
The angle between the line EC and the plane ABCD can be visualised in the diagram.

 We shoud calculate the length AG using Pythagoras' Theorem.
We shoud calculate the length AG using Pythagoras' Theorem.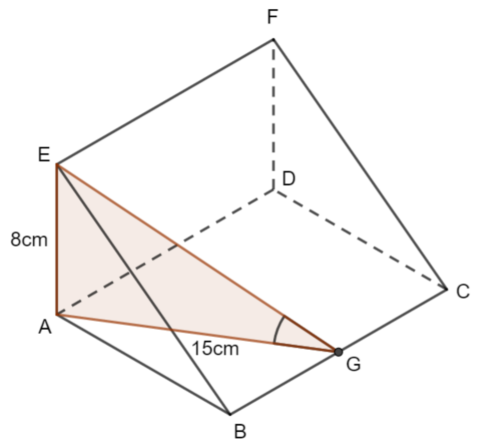 Here is the angle that we are required to find.
Here is the angle that we are required to find.
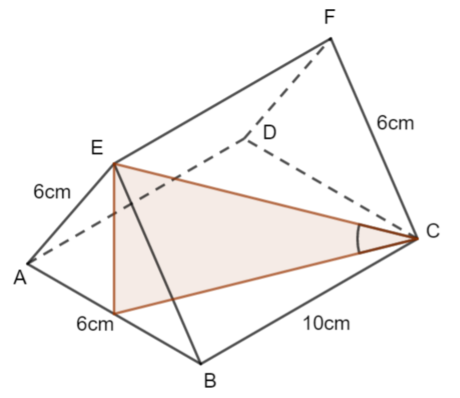
 a) WE can find the length EC using Pythagoras' Theorem
a) WE can find the length EC using Pythagoras' Theorem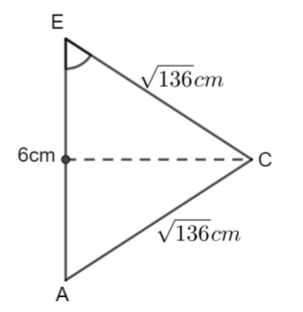 b) The length AC is the same as EC
b) The length AC is the same as EC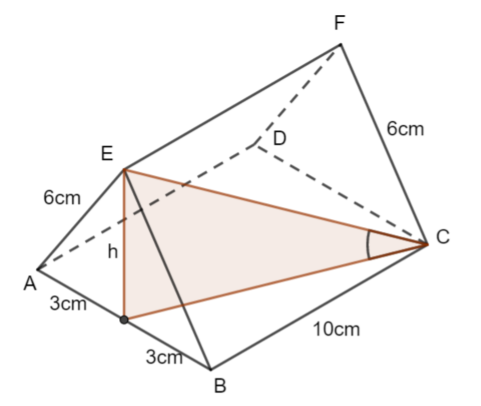 c) The angle between EC and the plane ABCD can be visualised in this diagram.
c) The angle between EC and the plane ABCD can be visualised in this diagram. Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn