On this page, you should learn about the double angle identities for sine and cosine
\(\large\sin(A+B)\equiv\sin A\cos B+ \cos A \sin B\\ \large\sin(A-B)\equiv\sin A\cos B- \cos A \sin B\)
\(\large\cos(A+B)\equiv\cos A\cos B- \sin A \sin B\\ \large\cos(A-B)\equiv\cos A\cos B+ \sin A \sin B\\\)
\(\large \tan(A+B)≡\frac{\tan A +\tan B}{1-\tan A\tan B}\\ \large \tan(A-B)≡\frac{\tan A -\tan B}{1+\tan A\tan B}\)
This quiz is about the Compound Angle formulae for sin(A+B) , cos(A+B) and tan(A+B)
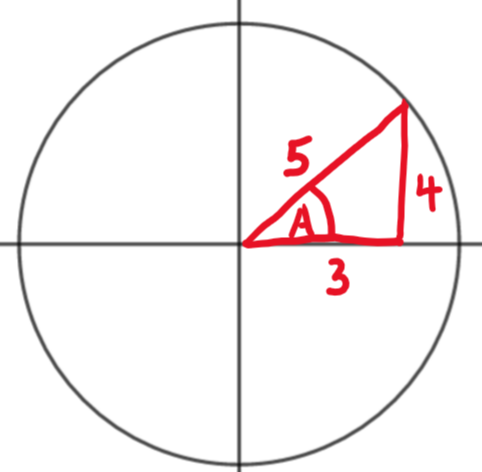
Find \(\large \sin (A+B)\) if A and B are acute angles such that
\(\large \sin A=\frac{3}{5}\\ \large \cos A=\frac{4}{5}\) and \(\large \sin B=\frac{5}{13}\\ \large \cos B=\frac{12}{13}\)
\(\large\sin(A+B)\equiv\sin A\cos B+ \cos A \sin B\)
\(\large\sin(A+B)=\frac{3}{5}\times\frac{12}{13}+\frac{4}{5}\times\frac{5}{13}=\frac{36+20}{65}=\frac{56}{65}\)
A and B are acute angles such that
\(\large \tan A=\frac{1}{4}\\ \large \tan B=\frac{3}{4}\)
If \(\large \tan(A+B)=\frac{a}{13}\) , find a
\(\large \tan(A+B)≡\frac{\tan A +\tan B}{1-\tan A\tan B}\)
\(\large \tan(A+B)=\frac{\frac{1}{4} +\frac{3}{4}}{1-\frac{1}{4} \times\frac{3}{4}}=\frac{1}{1-\frac{3}{16}}=\frac{1}{\frac{13}{16}}={\frac{16}{13}}\)
Find \(\large \cos (A-B)\) if A and B are angles such that
\(\large \sin A=-\frac{4}{5}\\ \large \cos A=-\frac{3}{5}\) and \(\large \sin B=\frac{7}{25}\\ \large \cos B=\frac{24}{25}\)
\(\large\cos(A-B)\equiv\cos A\cos B+ \sin A \sin B\\\)
\(\large\cos(A-B)=-\frac{3}{5}\times\frac{24}{25}+(-\frac{4}{5})\times\frac{7}{25}=\frac{-72-28}{125}=-\frac{100}{125}=-\frac{4}{5}\)
Find \(\large \tan (A+B)\) if A and B are angles such that
\(\large \tan A=-\frac{3}{4}\\ \large \tan B=\frac{2}{3}\)
\(\large \tan(A+B)≡\frac{\tan A +\tan B}{1-\tan A\tan B}\)
\(\large \tan(A+B)=\frac{-\frac{3}{4} +\frac{2}{3}}{1-(-\frac{3}{4}) \times\frac{2}{3}}=\frac{-\frac{1}{12}}{\frac{3}{2}}=-\frac{1}{18}\)
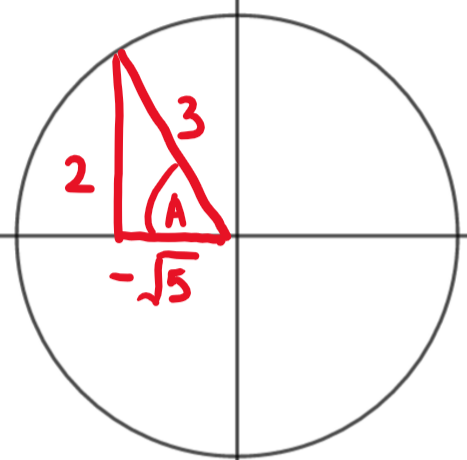
Find \(\large \sin (A+B)\) if A and B are acute angles such that
\(\large \sin A=\frac{\sqrt{7}}{4}\\ \large \cos A=\frac{3}{4}\) and \(\large \sin B=\frac{2}{3}\\ \large \cos B=\frac{\sqrt{5}}{3}\)
\(\large\sin(A+B)\equiv\sin A\cos B+ \cos A \sin B\)
\(\large\sin(A+B)=\frac{\sqrt{7}}{4}\times\frac{\sqrt{5}}{3}+\frac{3}{4}\times\frac{2}{3}=\frac{\sqrt{35}+6}{12}\)
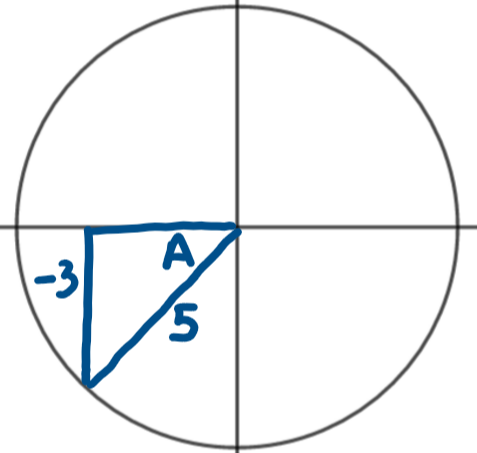
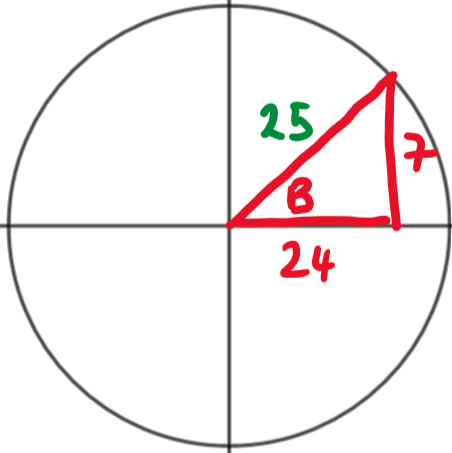
Find \(\large \sin (A-B)\) if A and B are angles represented as follows
\(\large\sin(A-B)\equiv\sin A\cos B- \cos A \sin B\)
\(\large\sin(A-B)=\frac{4}{5}\times(-\frac{5}{13})-\frac{3}{5}\times(-\frac{12}{13})=\frac{-20+36}{65}=\frac{16}{65}\)
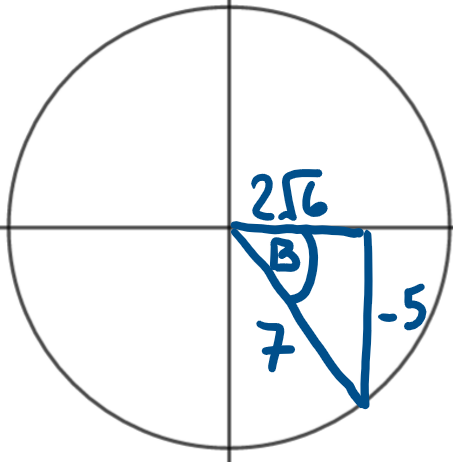
Find \(\large \sin (A+B)\) if A and B are angles represented as follows
\(\large\sin(A+B)\equiv\sin A\cos B+ \cos A \sin B\)
\(\large\sin(A+B)=\frac{2}{3}\times(\frac{2\sqrt{6}}{7})+(-\frac{\sqrt{5}}{3})\times(-\frac{5}{7})=\frac{4\sqrt{6}+5\sqrt{5}}{21}\)
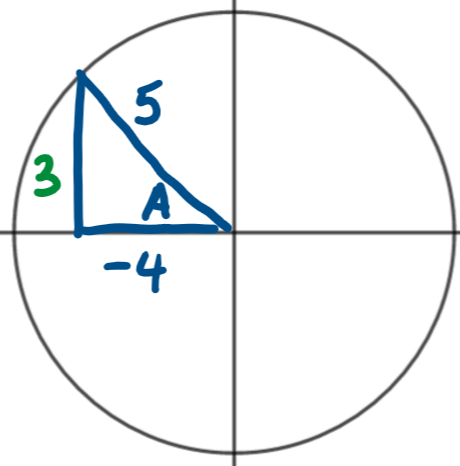
Find \(\large \cos(A+B)\) if A and B are angles represented as follows
\(\large\cos(A+B)\equiv\cos A\cos B- \sin A \sin B\\\)
\(\large\cos(A+B)=-\frac{4}{5}\times\frac{12}{13}-(-\frac{3}{5})\times\frac{5}{13}=\frac{-48+15}{65}=-\frac{33}{65}\)
If A and B are acute angles such that
\(\large \tan A=0.2\\ \large \tan B=0.5\)
Find a \(\large\tan(A+B)=\frac{a}{9}\)
\(\large \tan(A+B)≡\frac{\tan A +\tan B}{1-\tan A\tan B}\)
\(\large \tan(A+B)=\frac{0.2 +0.5}{1-0.2\times 0.5}={\frac{0.7}{0.9}}={\frac{7}{9}}\)
Find \(\large \cos (A-B)\) , given that
\(\large \cos A=-\frac{4}{5}\) , \(\large \frac{\pi}{2}\le A\le \pi\)
\(\large \tan B=\frac{7}{24}\) , \(0\le B\le \frac{\pi}{2}\)
Let's put the information into triangles and find the missing lengths using Pythagoras' Theorem
\(\large\cos(A-B)\equiv\cos A\cos B+ \sin A \sin B\\\)
\(\large\cos(A-B)=-\frac{4}{5}\times\frac{24}{25}+\frac{3}{5}\times\frac{7}{25}=\frac{-96+21}{125}=-\frac{75}{125}=-\frac{3}{5}\)
If \(\large \sin A=\frac{4}{5}\) , where \(\large 0\le A\le\frac{\pi}{2}\)
and \(\large \cos B=-\frac{12}{13}\) , where \(\large \pi \le B\le\frac{3\pi}{2}\)
work out \(\large \cos(B-A)\)
You will need to work out cosA and sinB
You will need to use the compound formula \(\large\cos(B-A)\equiv\cos B\cos A+ \sin B \sin A\)
If \(\large \sin(x+30°)=2\cos(x+60°)\) , then show that \(\large \tan x=\frac{\sqrt{3}}{9}\)
You will need to remember the exact values for sin30°, cos30°, sin60° and cos60°
a) By writing 15° as 45° - 30° , find the value of sin15°
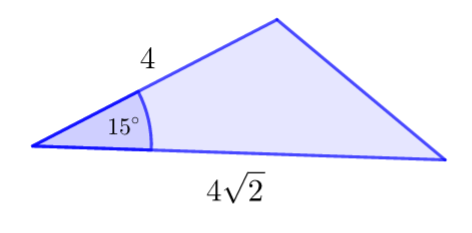
b) Hence , show that the area of this triangle \(\large =4(\sqrt{3}-1)\)
a) We need to use the compound angle formula to evaluate sin(45°-30°)
b) We need to use the area of the triangle formula. \(\large A= \frac{1}{2}ab\sin C\)
Prove that
\(\large \frac{\sin(A+B)+\sin(A-B)}{\cos(A+B)+\cos(A-B)}=\tan A\)
Prove that \(\large \tan 3x\equiv \frac{3\tan x-\tan^3x}{1-3\tan^2x}\)
Use the compound angle formula to work out \(\large \tan(2x + x)\)
Very careful manipulation is required in this question. Take your time to make sure that you do not make a mistake.
a) Write \(\large \cos4x\) in terms of \(\large\cos x\)
b) Hence , solve \(\large 8\cos^4x-8\cos^2x+1=\sin4x\) , for \(\large 0\le x\le\pi\)
a) Write \(\large\cos4x\equiv \cos(2x+2x)\) and use the double angle formula for \(\large \cos2x\) \(\large \sin2x\)
b) Remember that \(\large \tan x\equiv\frac{\sin x}{\cos x}\)
MY PROGRESS
Self-assessment How much of Compound Angle Formulae have you understood?
My notes
Which of the following best describes your feedback?
 In this page, we will will learn about the Compound Angle Formulae used in Trigonometry. These are really important because they open up so many other formulae in trigonometry. In particular, we can derive the double angle formula. There are 6 formula which are written in a shortened form in the IB formula booklet. You need to be very careful with positive/negative signs.
In this page, we will will learn about the Compound Angle Formulae used in Trigonometry. These are really important because they open up so many other formulae in trigonometry. In particular, we can derive the double angle formula. There are 6 formula which are written in a shortened form in the IB formula booklet. You need to be very careful with positive/negative signs.




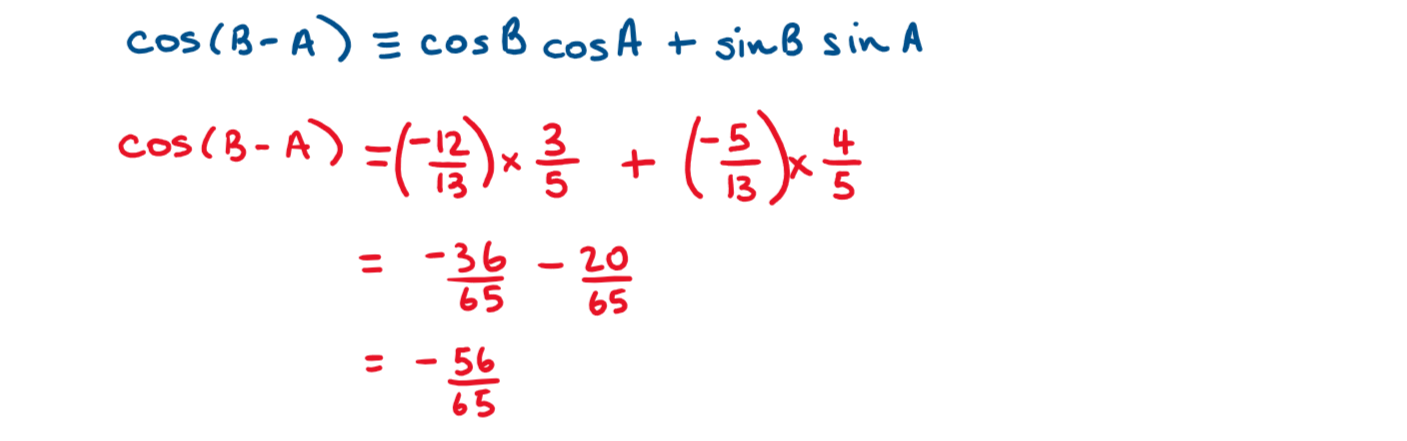



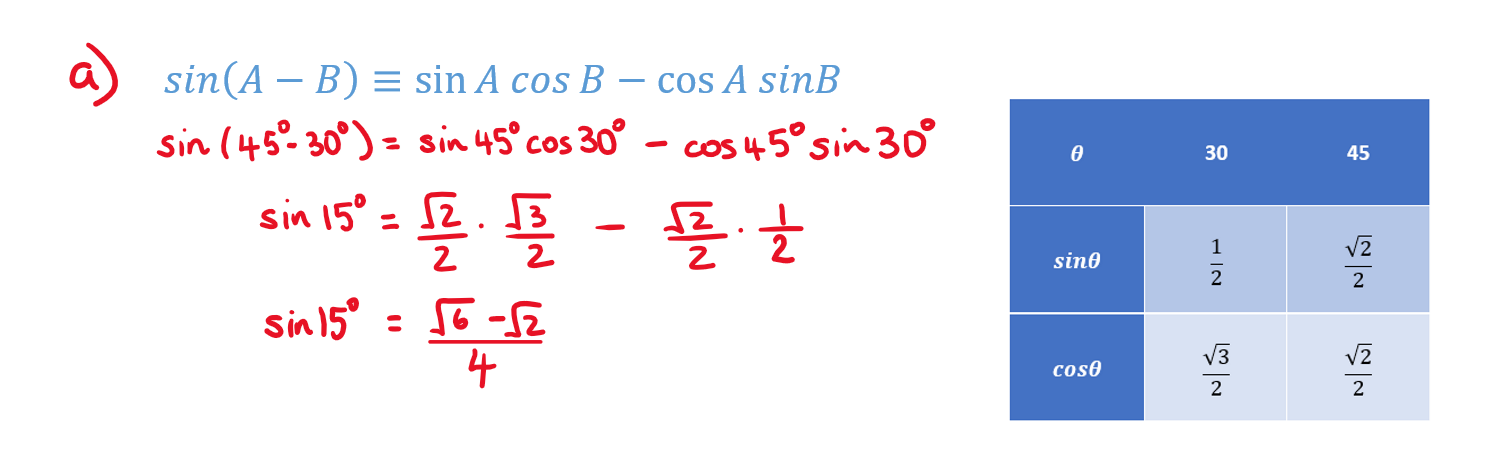
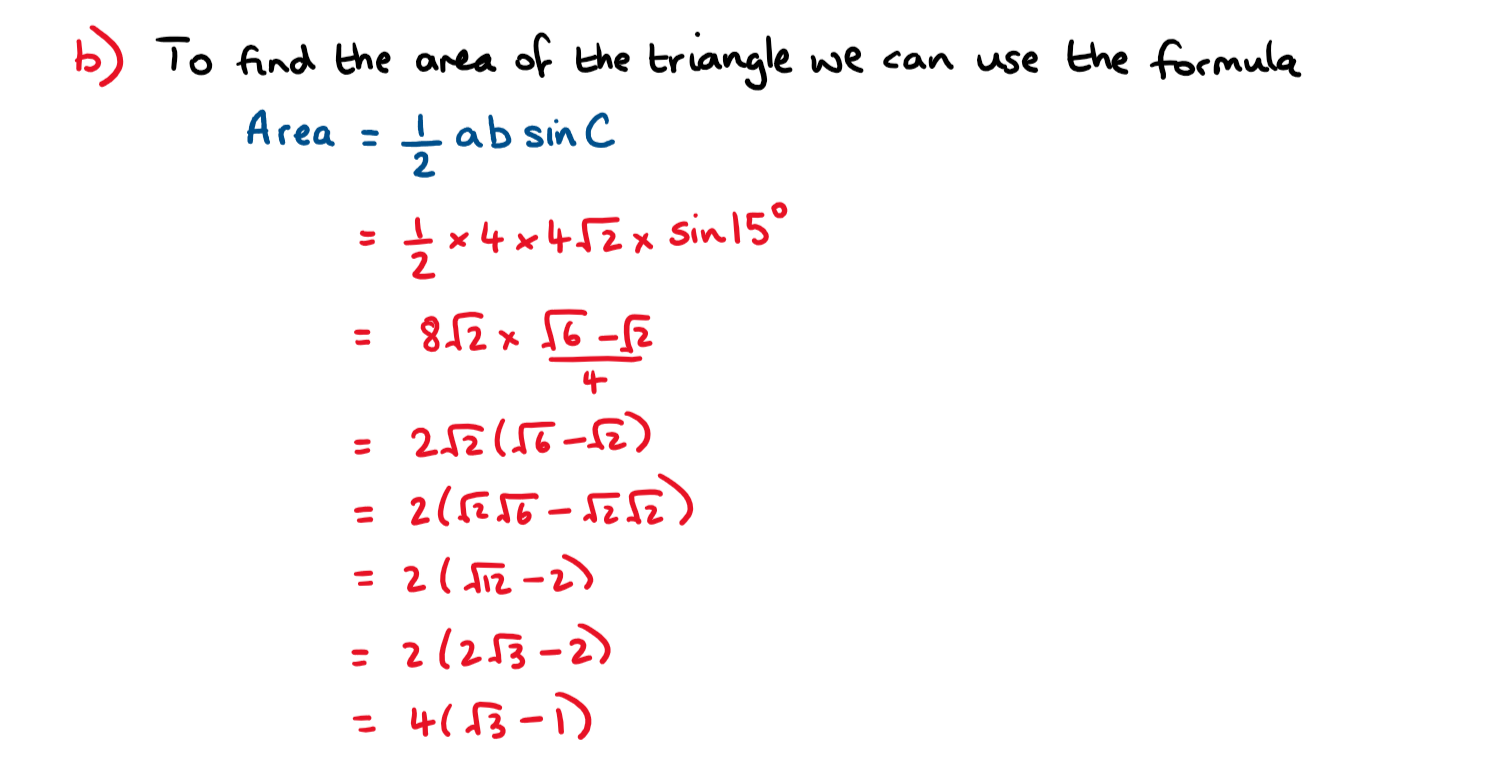








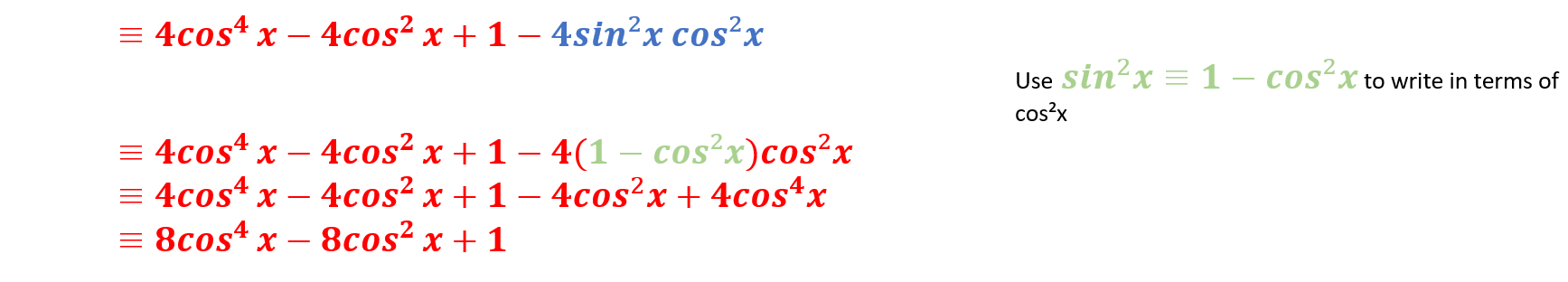


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn