 In this page, we will learn about the graphs of the circular functions sinx, cosx and tanx. We will link this to work that we have done on Transforming Functions to see how translating and stretching the graphs affect the tigonometric functions. It is fairly common to get a long question on this topic in the exam and they can come up on paper 1 or paper 2, so you need to be comfortable using your calculator and working without it. You can find typical questions in the exam-style questions section.
In this page, we will learn about the graphs of the circular functions sinx, cosx and tanx. We will link this to work that we have done on Transforming Functions to see how translating and stretching the graphs affect the tigonometric functions. It is fairly common to get a long question on this topic in the exam and they can come up on paper 1 or paper 2, so you need to be comfortable using your calculator and working without it. You can find typical questions in the exam-style questions section.
On this page, you should learn about
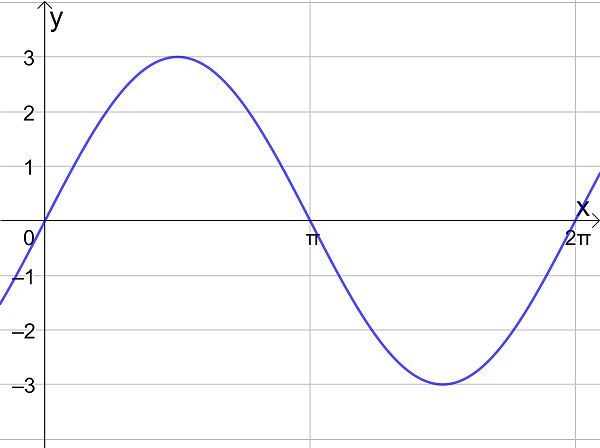
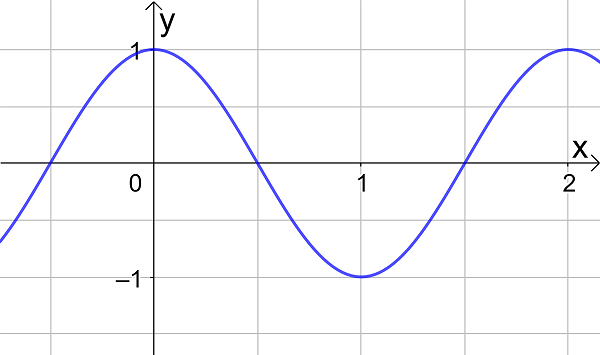
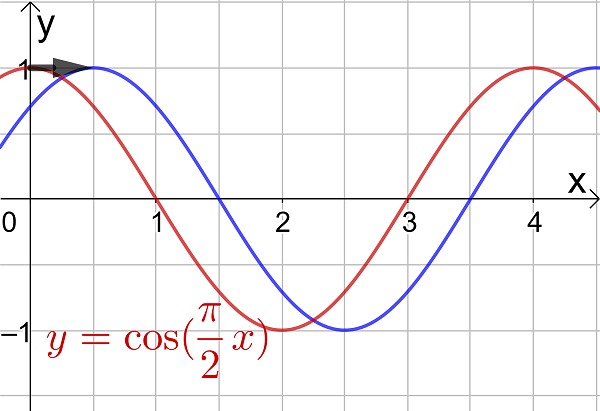
- the graphs of the functions sinx, cosx and tanx
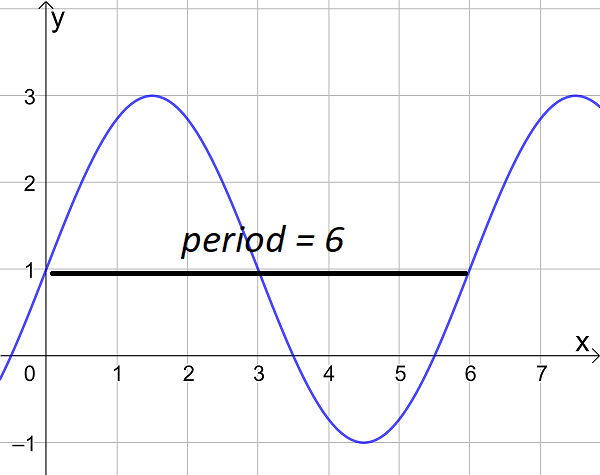
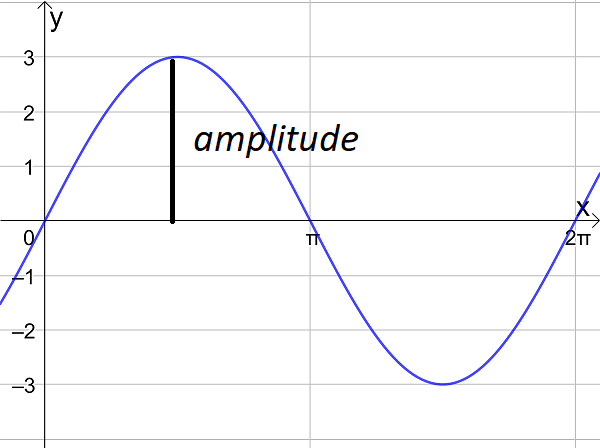
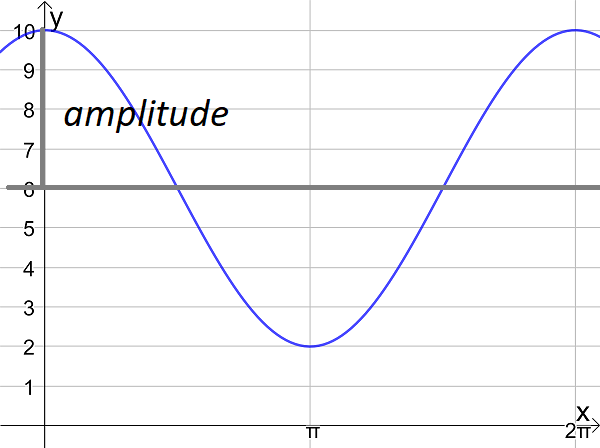
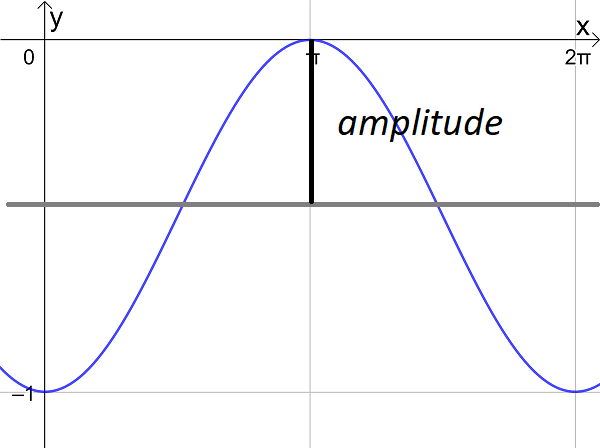
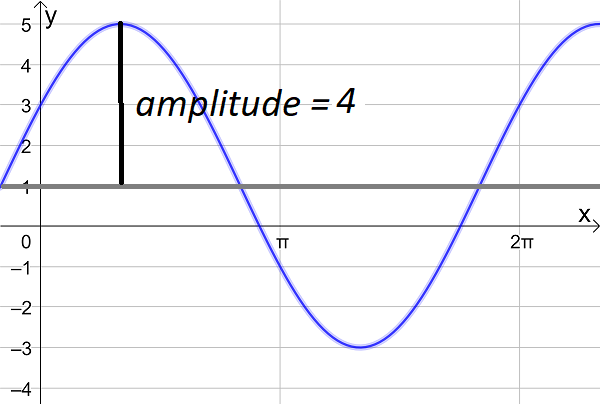
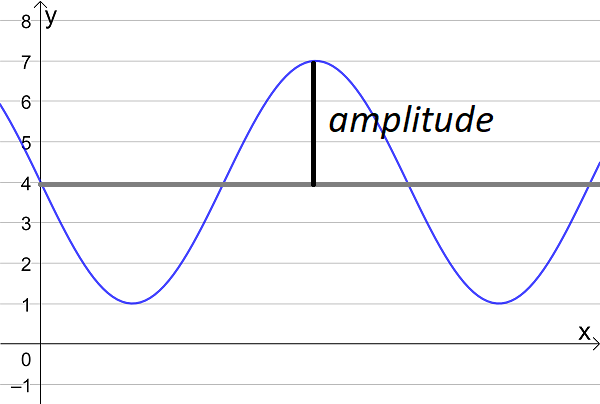
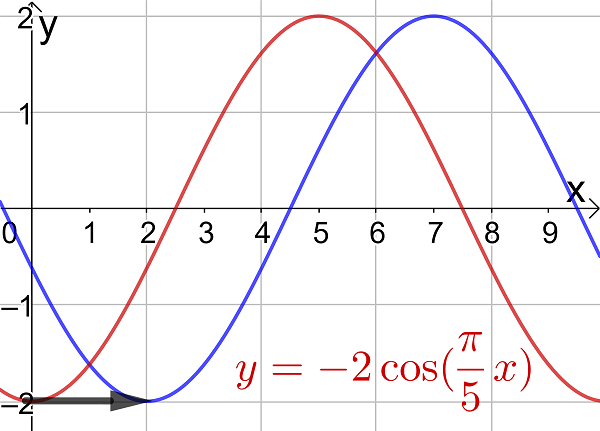
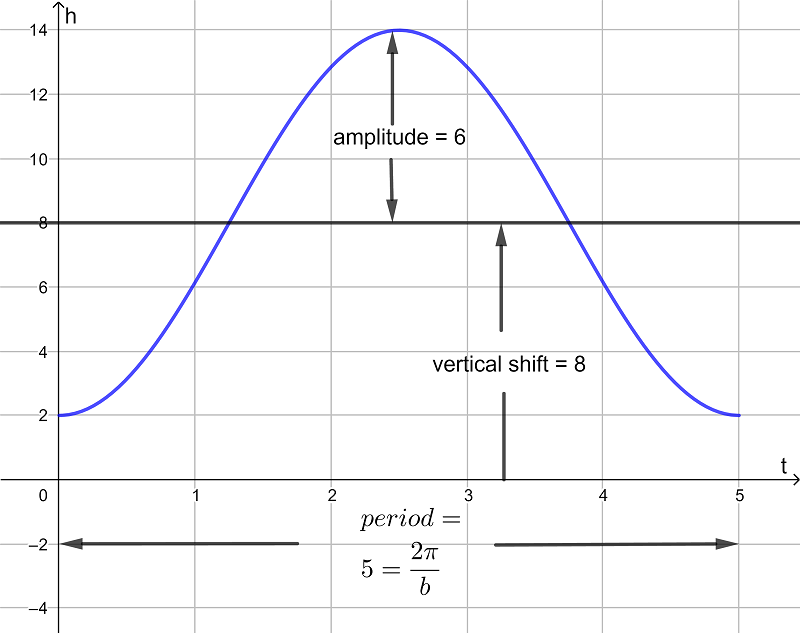
- the amplitude and period of a trigonometric graph
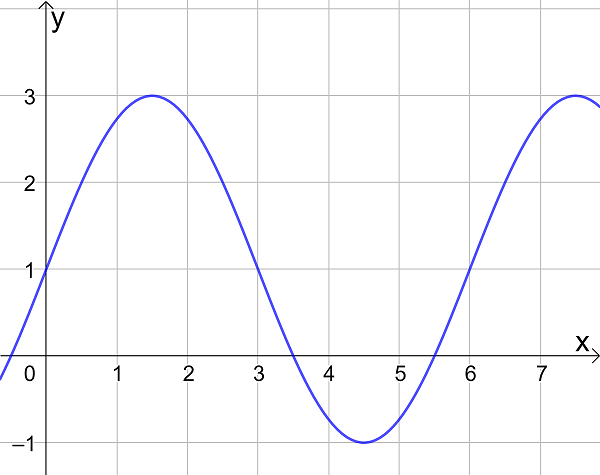
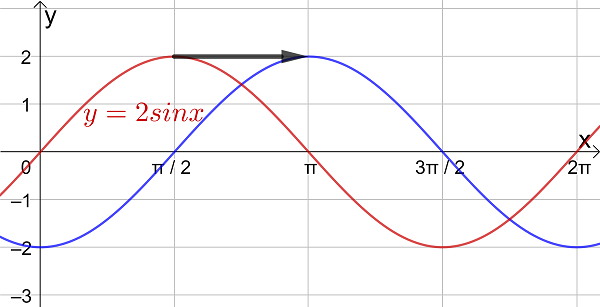
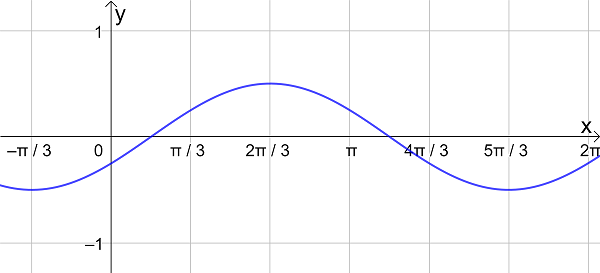
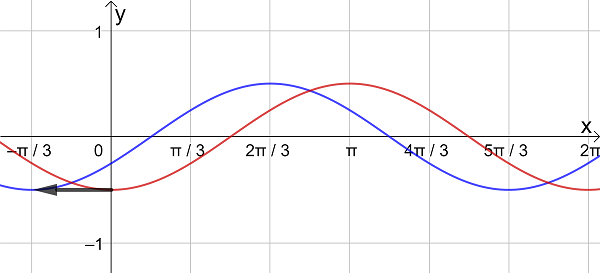
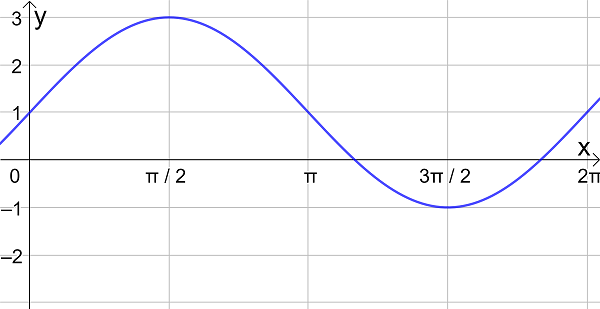
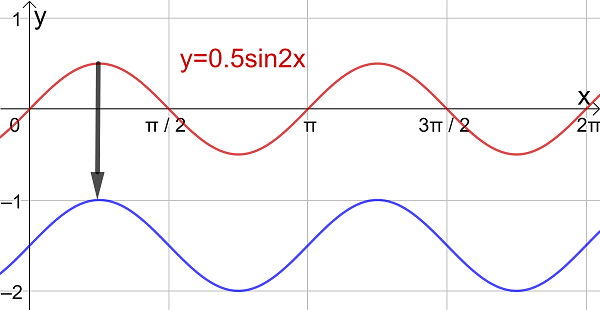
- Composite functions of the form \(\large f(x) = a \sin(b(x+c))+d\) and \(\large f(x) = a \cos(b(x+c))+d\)
- Transformations of trigonometric functions
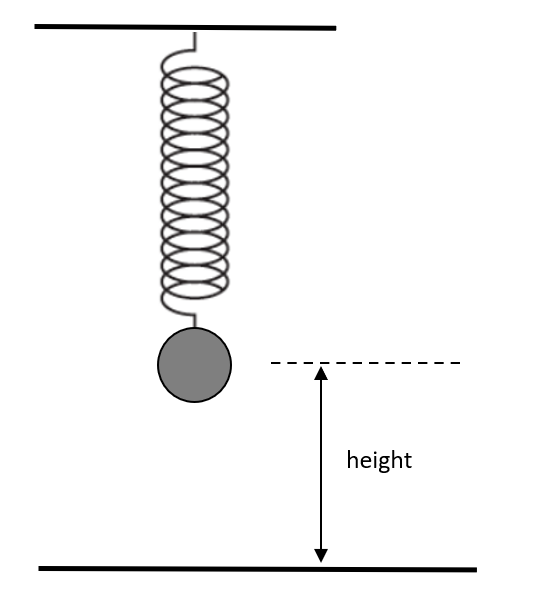
- Modelling with trigonometric functions
Here is a quiz about the period of a trigonometric function
START QUIZ!
Here is a quiz about the amplitude of a trigonometric function
START QUIZ!
Here is a quiz about translations of a trigonometric function
START QUIZ!


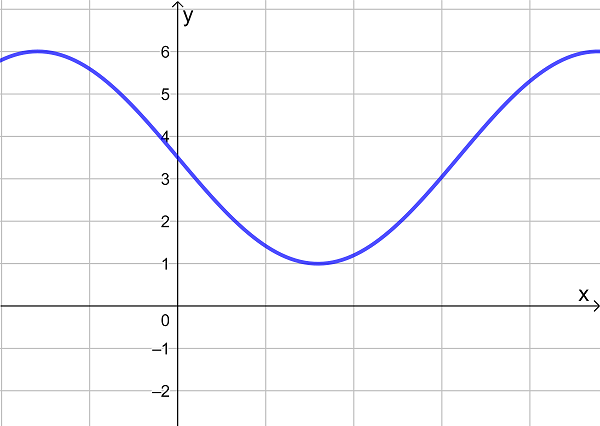
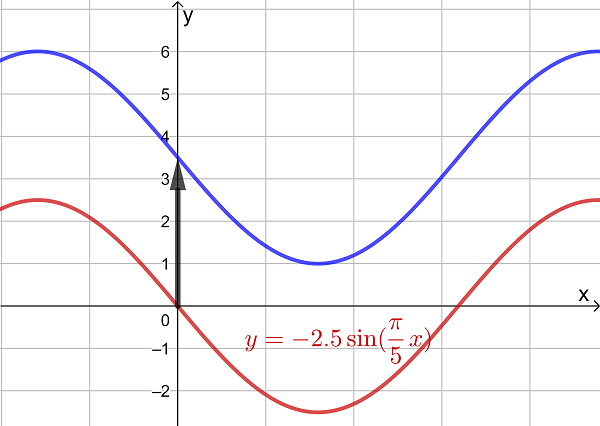
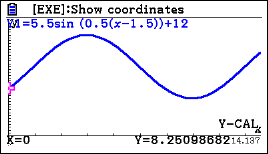
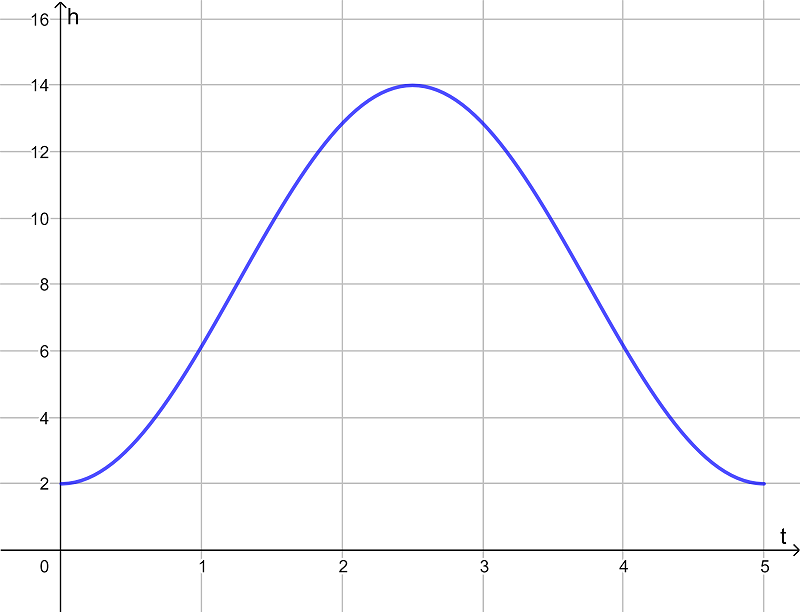
The height h of water, in metres, in a habour is modelled by the function \(\large h(t)=5.5\sin(0.5(t-1.5))+12\) where t is time after midday in hours.
a) Find the initial height of the water.
b) At what time is it when the water reaches this height again?
c) Find the maximum height of the water.
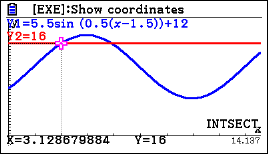
d) How much time is there in between the first and second time that the water at 16 metres?
Give heights to 3 significant figures and times to the nearest minute
Hint
Full Solution
How much of Trigonometric Graphs have you understood?




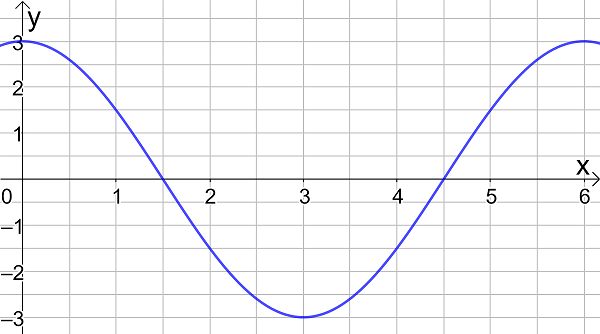
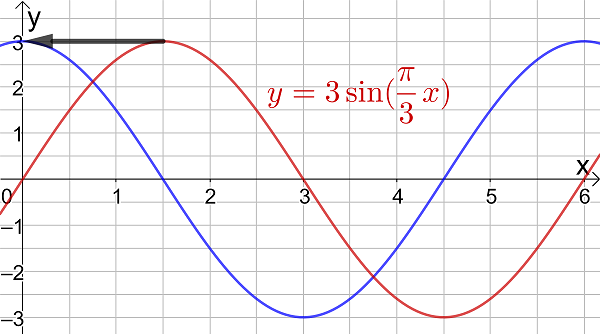

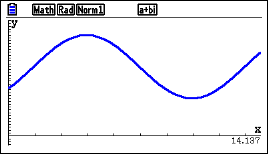

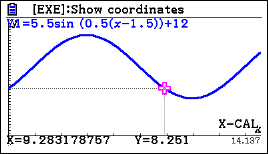 0.283x60 = 17 minutes
0.283x60 = 17 minutes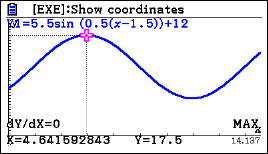






 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn