 In this page, we will look at finding the volume and surface area of three-dimensional solids. The formulae for these solids can all be found in the formula booklet. You just need to know where to find them, as some are in the prior learning section and some are in the geometry and trigonometry section.
In this page, we will look at finding the volume and surface area of three-dimensional solids. The formulae for these solids can all be found in the formula booklet. You just need to know where to find them, as some are in the prior learning section and some are in the geometry and trigonometry section.
On this page, you should learn about volumes and surface areas of
- pyramids
- cones
- spheres
- hemispheres
Here is a quiz that practises the skills from this page
START QUIZ!
3D Solids 1 1/1
 What is the volume of a sphere with radius 4cm?
What is the volume of a sphere with radius 4cm?
\(\large V=\frac{4}{3}\pi r^3\\ \large V=\frac{4}{3}\pi \times4^3=\frac{256\pi}{3}\)
 What is the surface of a sphere with radius 4cm?
What is the surface of a sphere with radius 4cm?
\(\large A=4\pi r^2\\ \large A=4\pi\times 4^2=64\pi\)
 The diameter of Europa, one of the moons of Jupiter, is approaximately \(\large 3\times 10^6\ m\).
The diameter of Europa, one of the moons of Jupiter, is approaximately \(\large 3\times 10^6\ m\).
Assuming that the moon is spherical in shape, the volume is calculated to be \(\large \pi \times a\times 10^{18}\ m^3\).
Find the value of a
a =
\(\large V=\frac{4}{3}\pi r^3\\ \large V=\frac{4}{3}\pi \times(1.5\times10^6)^3=\pi\times4.5\times10^{18}\)
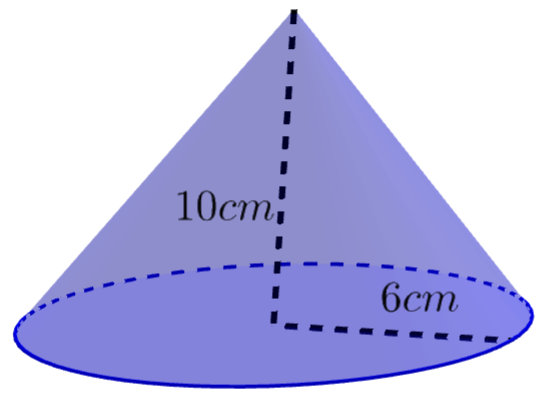 A cone has radius 6cm and height 10cm.
A cone has radius 6cm and height 10cm.
The volume of the cone is \(\large a \times \pi \ cm^3\)
Find the value of a
a =
\(\large V=\frac{1}{3}\pi r^2h\\ \large V=\frac{1}{3}\pi \times6^2\times10=120\pi\)
 A hemisphere has radius = 3cm.
A hemisphere has radius = 3cm.
The volume of the solid is \(\large a\times \pi \ cm^3\)
Find the value of a
a =
\(\large V=\frac{2}{3}\pi r^3\\ \large V=\frac{2}{3}\pi \times3^3=18\pi\)
 A sphere has radius 8cm.
A sphere has radius 8cm.
The surface area of the solid is \(\large a\times \pi \ cm^3\)
Find the value of a
a =
\(\large A=4 \pi r^2\\ \large A=4\pi\times8^2=256\pi\)
 A hemisphere has diameter = 10cm.
A hemisphere has diameter = 10cm.
The total surface area of the solid is \(\large a\times \pi \ cm^2\)
Find the value of a
a =
The surface area of a hemisphere is made up of the curved surface and the circular base
\(\large A=2\pi r^2+\pi r^2\\\large A=3\pi r^2\\ \large A=3\pi\times 5^2=75\pi\)
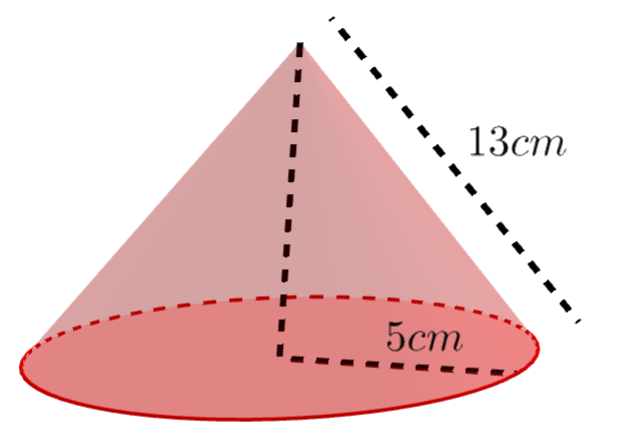 A cone has radius 5cm and slant height = 13cm.
A cone has radius 5cm and slant height = 13cm.
The total surface area of this cone is \(\large a\times \pi \ cm^2\)
Find the value of a
a =
The surface of the cone is made of two parts, the curved surface and the circular base
\(\large A=\pi rl+\pi r^2\\\large A=\pi\times5\times13+\pi\times5^2=90\pi\)
A sphere has a volume of \(\large 972\pi \ cm^3\)
Work out the radius of the sphere.
r =
\(\large V=\frac{4}{3}\pi r^3\\ \large 972\pi=\frac{4}{3}\pi \times r^3\\ \large r^3=729\\ \large r=9\)
 A cone with a height of 12cm has a volume of \(\large 100\pi \ cm^3\)
A cone with a height of 12cm has a volume of \(\large 100\pi \ cm^3\)
Find the value of r, the radius of the base of the cone.
r =
\(\large V=\frac{1}{3}\pi r^2h\\ \large 100\pi=\frac{1}{3}\pi \times r^2\times 12\\ \large r^2=25\\ \large r=5\)
text


A glass is made up of a hemisphere and a cone.
Find the volume of the glass.
Give your answer to 3 significant figures
Hint
The radius of the cone and the hemisphere are both 5cm
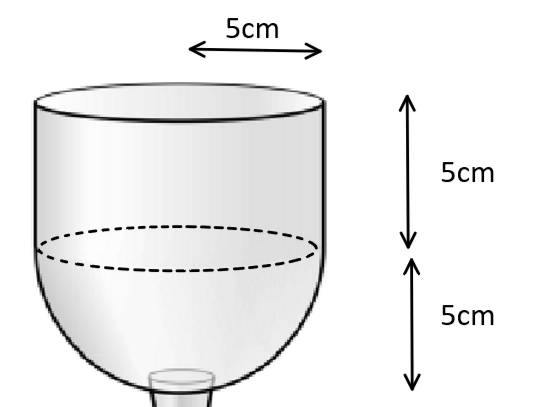
Full Solution
 The radius of the cone and the hemisphere are both 5cm
The radius of the cone and the hemisphere are both 5cm
Volume of cone,
\(\large V_{cone}=\pi r^2h\\ \large V_{cone}=\pi \times5^2\times 5\\ \large V_{cone}=125\pi \)
Volume of hemisphere,
\(\large V_{hemisphere}=2\pi r^2\\ \large V_{hemisphere}=2\times \pi \times 5^2\\ \large V_{hemisphere}=50\pi\)
Total Volume\(\large=125\pi+50\pi\\ \large=175\pi\\ \large\approx549.779...cm^3\\ \large\approx550cm^3\)




The total surface area of a hemisphere is 1360 cm²
Find the radius.
Give your answer to 3 significant figures.
Hint
The surface of a hemisphere is made of two parts
- the curved surface
- the circular base
Full Solution
The surface area of a hemisphere,
\(\large A=\pi r^2+\pi r^2\\ \large A=3\pi r^2\\ \large 1360=3\pi r^2\\ \large r^2=\frac{1360}{3\pi}\\ \large r=\sqrt{\frac{1360}{3\pi}}\\ \large r\approx12.0125...\\ \large r\approx12.0cm \)


a) A sphere has a radius of 10cm. Find the volume, giving your answer in terms of \(\large \pi\).
b) A cone has the same volume and the same radius as the sphere. Find the height of the cone.
c) Another sphere and cone have the same volume and the same radius, r. Find an equation for the height of the cone, h in terms of r.
Hint
c) Solve \(\large \frac{4}{3}\pi r^3=\frac{1}{3}\pi r^2h\\\)
Full Solution
a)
\(\large V=\frac{4}{3}\pi r^3\\ \large V=\frac{4}{3}\pi \times10^3\\ \large V=\frac{4000}{3}\pi \ cm^3\)
b)
\(\large V=\frac{1}{3}\pi r^2h\\ \large \frac{4000}{3}\pi=\frac{1}{3}\pi \times 10^2\times h\\ \large h=40\ cm\)
c)
\(\large \frac{4}{3}\pi r^3=\frac{1}{3}\pi r^2h\\ \large \frac{4}{\rlap{/}3}\rlap{/}\pi r^3=\frac{1}{\rlap{/}3}\rlap{/}\pi r^2h\\ \large 4r^3=r^2h\\ \large 4r=h\\ \large h=4r\)


Three metal spheres have radii 1cm, 6cm and 8cm.
The spheres are melted down and made into one bigger sphere.
What is the radius of the single sphere?

Hint
Full Solution
The volume of a sphere is given by \(\large V=\frac{4}{3}\pi r^3\)
The Volume of the three spheres is
\(\large V=\frac{4}{3}\pi \times1^3+\frac{4}{3}\pi \times 6^3+\frac{4}{3}\pi \times 8^3\\ \large V=\frac{4}{3}\pi \times(1^3+6^3+8^3)\\ \large V=\frac{4}{3}\pi \times(729)\\ \)
The large sphere has the same volume as these three spheres
\(\large \frac{4}{3}\pi \times R^3=\frac{4}{3}\pi \times(729)\\ \large R^3=729\\ \large R=9\ cm \)


A cylindrical metal bar with height 12cm and diameter 12cm is melted down and made into spheres of diameter 3cm.
How many spheres will it make?
Hint
Full Solution
The volume of the cylindrical bar is
\(\large V=\frac{1}{3}\pi\times 6^2\times12\\ \large V=144\pi \)
The volume of one of the spheres is
\(\large V=\frac{4}{3}\pi\times 1.5^3\\ \large V=4.5\pi \)
Therefore, the number of spheres is \(\large \frac{144\pi}{4.5\pi}\)
\(\large 32\) spheres
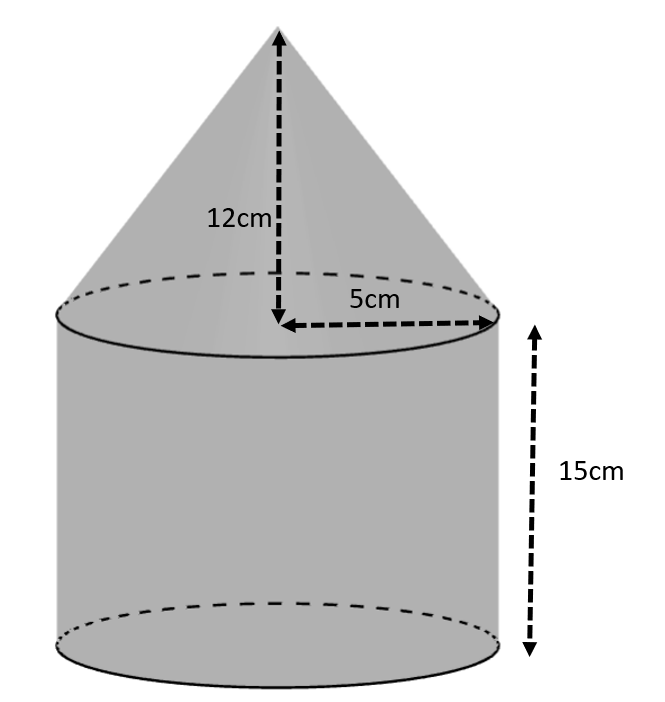


A solid is made up of a cone and a cylinder.
The radius is 5cm, the height of the cone is 12cm and the height of the cylinder is 15cm.
Show that the total surface area of the solid is \(\large 240\pi\)
Hint
There are three surfaces to find: the curved surface of the cone, the curved surface of the cylinder and the circular base.
To find the curved surface area of the cone, you need to find the slant height. Use Pythagoras' Theorem.
Full Solution
 We need to find the slant height of the cone:
We need to find the slant height of the cone:
\(\large l^2=5^2+12^2\\ \large l^2=169\\ \large l=13\)
The surface area of the cone is
\(\large A_{cone}=\pi rl\\ \large A_{cone}=\pi\times5\times 13\\ \large A_{cone}=65\pi\)
The surface area of the cylinder is
\(\large A_{cylinder}=2\pi rh\\ \large A_{cylinder}=2\pi \times 5\times 15\\ \large A_{cylinder}=150\pi\)
The area of the base is
\(\large A_{base}=\pi r^2\\ \large A_{base}=\pi \times 5^2\\ \large A_{base}=25\pi \)
The total surface area is
\(\large =65\pi+150\pi+25\pi\\ \large=240\pi\)
How much of 3-Dimensional Solids have you understood?
Feedback
Which of the following best describes your feedback?



 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn