| Date | May 2017 | Marks available | 4 | Reference code | 17M.2.sl.TZ2.4 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The quadrilateral ABCD represents a park, where \({\text{AB}} = 120{\text{ m}}\), \({\text{AD}} = 95{\text{ m}}\) and \({\text{DC}} = 100{\text{ m}}\). Angle DAB is 70° and angle DCB is 110°. This information is shown in the following diagram.
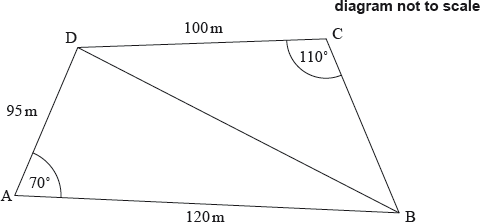
A straight path through the park joins the points B and D.
A new path, CE, is to be built such that E is the point on BD closest to C.
The section of the park represented by triangle DCE will be used for a charity race. A track will be marked along the sides of this section.
Find the length of the path BD.
Show that angle DBC is 48.7°, correct to three significant figures.
Find the area of the park.
Find the length of the path CE.
Calculate the total length of the track.
Markscheme
\(({\text{B}}{{\text{D}}^2} = ){\text{ }}{95^2} + {120^2} - 2 \times 95 \times 120 \times \cos 70^\circ \) (M1)(A1)
Note: Award (M1) for substituted cosine rule, (A1) for correct substitution.
\(({\text{BD}} = ){\text{ }}125{\text{ (m) }}\left( {125.007 \ldots {\text{ (m)}}} \right)\) (A1)(G2)
[3 marks]
\(\frac{{\sin {\text{DBC}}}}{{100}} = \frac{{\sin 110^\circ }}{{125.007 \ldots }}\) (M1)(A1)(ft)
Note: Award (M1) for substituted sine rule, (A1)(ft) for correct substitution.
Follow through from their answer to part (a).
\(({\text{DBC}} = ){\text{ }}48.7384 \ldots ^\circ \) (A1)(ft)
\(({\text{DBC}} = ){\text{ }}48.7^\circ \) (AG)
Notes: Award the final (A1)(ft) only if both their unrounded answer and 48.7° is seen. Follow through from their answer to part (a), only if their unrounded answer rounds to 48.7°.
[3 marks]
\(\frac{1}{2} \times 125.007 \ldots \times 100 \times \sin 21.3^\circ + \frac{1}{2} \times 95 \times 120 \times \sin 70^\circ \) (A1)(M1)(M1)
Note: Award (A1) for 21.3° (21.2615…) seen, (M1) for substitution into (at least) one area of triangle formula in the form \(\frac{1}{2}ab\sin c\), (M1) for their correct substitutions and adding the two areas.
\(7630{\text{ }}{{\text{m}}^2}{\text{ }}(7626.70 \ldots {{\text{m}}^2})\) (A1)(ft)(G3)
Notes: Follow through from their answers to part (a). Accept \(7620{\text{ }}{{\text{m}}^2}{\text{ }}(7622.79 \ldots {{\text{m}}^2})\) from use of 48.7384…
[4 marks]
\(({\text{CE}} = ){\text{ }}100 \times \sin 21.3^\circ \) (M1)
\(({\text{CE}} = ){\text{ }}36.3{\text{ (m) }}\left( {36.3251 \ldots {\text{ (m)}}} \right)\) (A1)(ft)(G2)
Note: Follow through from their angle 21.3° in part (c). Award (M0)(A0) for halving 110° and/or assuming E is the midpoint of BD in any method seen.
OR
\({\text{area of BCD}} = \frac{1}{2}{\text{BD}} \times {\text{CE}}\) (M1)
\(({\text{CE}} = ){\text{ }}36.3{\text{ (m) }}\left( {36.3251 \ldots {\text{ (m)}}} \right)\) (A1)(ft)(G2)
Note: Follow through from parts (a) and (c). Award (M0)(A0) for halving 110° and/or assuming E is the midpoint of BD in any method seen.
[2 marks]
\(\sqrt {{{100}^2} - 36.3251{ \ldots ^2}} + 100 + 36.3251 \ldots \) (M1)(M1)
Note: Award (M1) for correct use of Pythagoras to find DE (or correct trigonometric equation, \(100 \times \cos 21.3\), to find DE), (M1) for the sum of 100, their DE and their CE.
\(229{\text{ (m) }}\left( {229.494 \ldots {\text{ (m)}}} \right)\) (A1)(ft)(G2)
Note: Follow through from part (d). Use of 3 sf values gives an answer of \(230{\text{ (m) }}\left( {229.5{\text{ (m)}}} \right)\).
[3 marks]

