| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.sl.TZ1.2 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Write down | Question number | 2 | Adapted from | N/A |
Question
The base of an electric iron can be modelled as a pentagon ABCDE, where:
\[\begin{array}{*{20}{l}} {{\text{BCDE is a rectangle with sides of length }}(x + 3){\text{ cm and }}(x + 5){\text{ cm;}}} \\ {{\text{ABE is an isosceles triangle, with AB}} = {\text{AE and a height of }}x{\text{ cm;}}} \\ {{\text{the area of ABCDE is 222 c}}{{\text{m}}^{\text{2}}}{\text{.}}} \end{array}\]
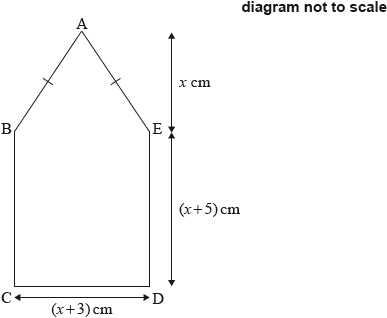
Insulation tape is wrapped around the perimeter of the base of the iron, ABCDE.
F is the point on AB such that \({\text{BF}} = {\text{8 cm}}\). A heating element in the iron runs in a straight line, from C to F.
Write down an equation for the area of ABCDE using the above information.
Show that the equation in part (a)(i) simplifies to \(3{x^2} + 19x - 414 = 0\).
Find the length of CD.
Show that angle \({\rm{B\hat AE}} = 67.4^\circ \), correct to one decimal place.
Find the length of the perimeter of ABCDE.
Calculate the length of CF.
Markscheme
\(222 = \frac{1}{2}x(x + 3) + (x + 3)(x + 5)\) (M1)(M1)(A1)
Note: Award (M1) for correct area of triangle, (M1) for correct area of rectangle, (A1) for equating the sum to 222.
OR
\(222 = (x + 3)(2x + 5) - 2\left( {\frac{1}{4}} \right)x(x + 3)\) (M1)(M1)(A1)
Note: Award (M1) for area of bounding rectangle, (M1) for area of triangle, (A1) for equating the difference to 222.
[2 marks]
\(222 = \frac{1}{2}{x^2} + \frac{3}{2}x + {x^2} + 3x + 5x + 15\) (M1)
Note: Award (M1) for complete expansion of the brackets, leading to the final answer, with no incorrect working seen. The final answer must be seen to award (M1).
\(3{x^2} + 19x - 414 = 0\) (AG)
[2 marks]
\(x = 9{\text{ }}\left( {{\text{and }}x = - \frac{{46}}{3}} \right)\) (A1)
\({\text{CD}} = 12{\text{ (cm)}}\) (A1)(G2)
[2 marks]
\(\frac{1}{2}({\text{their }}x + 3) = 6\) (A1)(ft)
Note: Follow through from part (b).
\(\tan \left( {\frac{{{\rm{B\hat AE}}}}{2}} \right) = \frac{6}{9}\) (M1)
Note: Award (M1) for their correct substitutions in tangent ratio.
\({\rm{B\hat AE}} = 67.3801 \ldots ^\circ \) (A1)
\( = 67.4^\circ \) (AG)
Note: Do not award the final (A1) unless both the correct unrounded and rounded answers are seen.
OR
\(\frac{1}{2}({\text{their }}x + 3) = 6\) (A1)(ft)
\(\tan ({\rm{A\hat BE}}) = \frac{9}{6}\) (M1)
Note: Award (M1) for their correct substitutions in tangent ratio.
\({\rm{B\hat AE}} = 180^\circ - 2({\rm{A\hat BE}})\)
\({\rm{B\hat AE}} = 67.3801 \ldots ^\circ \) (A1)
\( = 67.4^\circ \) (AG)
Note: Do not award the final (A1) unless both the correct unrounded and rounded answers are seen.
[3 marks]
\(2\sqrt {{9^2} + {6^2}} + 12 + 2(14)\) (M1)(M1)
Note: Award (M1) for correct substitution into Pythagoras. Award (M1) for the addition of 5 sides of the pentagon, consistent with their \(x\).
\(61.6{\text{ (cm) }}\left( {61.6333 \ldots {\text{ (cm)}}} \right)\) (A1)(ft)(G3)
Note: Follow through from part (b).
[3 marks]
\({\rm{F\hat BC}} = 90 + \left( {\frac{{180 - 67.4}}{2}} \right){\text{ }}( = 146.3^\circ )\) (M1)
OR
\(180 - \frac{{67.4}}{2}\) (M1)
\({\rm{C}}{{\text{F}}^2} = {8^2} + {14^2} - 2(8)(14)\cos (146.3^\circ )\) (M1)(A1)(ft)
Note: Award (M1) for substituted cosine rule formula and (A1) for correct substitutions. Follow through from part (b).
\({\text{CF}} = 21.1{\text{ (cm) }}(21.1271 \ldots )\) (A1)(ft)(G3)
OR
\({\rm{G\hat BF}} = \frac{{67.4}}{2} = 33.7^\circ \) (A1)
Note: Award (A1) for angle \({\rm{G\hat BF}} = 33.7^\circ \), where G is the point such that CG is a projection/extension of CB and triangles BGF and CGF are right-angled triangles. The candidate may use another variable.
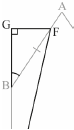
\({\text{GF}} = 8\sin 33.7^\circ = 4.4387 \ldots \)\(\,\,\,\)AND\(\,\,\,\)\({\text{BG}} = 8\cos 33.7^\circ = 6.6556 \ldots \) (M1)
Note: Award (M1) for correct substitution into trig formulas to find both GF and BG.
\({\text{C}}{{\text{F}}^2} = {(14 + 6.6556 \ldots )^2} + {(4.4387 \ldots )^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras formula to find CF.
\({\text{CF}} = 21.1{\text{ (cm) }}(21.1271 \ldots )\) (A1)(ft)(G3)
[4 marks]

