| Date | November 2014 | Marks available | 4 | Reference code | 14N.2.sl.TZ0.4 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find and Show that | Question number | 4 | Adapted from | N/A |
Question
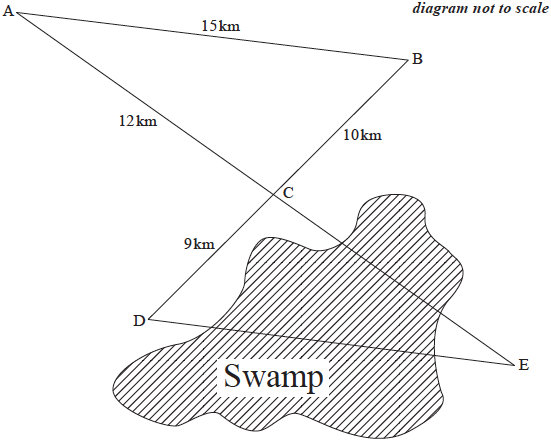
A surveyor has to calculate the area of a triangular piece of land, DCE.
The lengths of CE and DE cannot be directly measured because they go through a swamp.
AB, DE, BD and AE are straight paths. Paths AE and DB intersect at point C.
The length of AB is 15 km, BC is 10 km, AC is 12 km, and DC is 9 km.
The following diagram shows the surveyor’s information.
(i) Find the size of angle \({\rm{ACB}}\).
(ii) Show that the size of angle \({\rm{DCE}}\) is \(85.5^\circ\), correct to one decimal place.
The surveyor measures the size of angle \({\text{CDE}}\) to be twice that of angle \({\text{DEC}}\).
(i) Using angle \({\text{DCE}} = 85.5^\circ \), find the size of angle \({\text{DEC}}\).
(ii) Find the length of \({\text{DE}}\).
Calculate the area of triangle \({\text{DEC}}\).
Markscheme
(i) \(\cos {\rm{A\hat CB}} = \frac{{{{10}^2} + {{12}^2} - {{15}^2}}}{{2 \times 10 \times 12}}\) (M1)(A1)
Note: Award (M1) for substituted cosine rule,
(A1) for correct substitution.
\({\rm{A\hat CB}} = 85.5^\circ \;\;\;({\text{85.4593}} \ldots {\text{)}}\) (A1)(G2)
(ii) \({\rm{D\hat CE}} = {\rm{A\hat CB}}\;\;\;{\text{and}}\;\;\;{\rm{A\hat CB}} = 85.5^\circ \;\;\;({\text{85.4593}} \ldots ^\circ {\text{)}}\) (A1)
OR
\({\rm{B\hat CE}} = 180^\circ - 85.5^\circ = 94.5^\circ \;\;\;{\text{and}}\;\;\;{\rm{D\hat CE}} = 180^\circ - 94.5^\circ = 85.5^\circ \) (A1)
Notes: Both reasons must be seen for the (A1) to be awarded.
\({\rm{D\hat CE}} = 85.5^\circ \) (AG)
(i) \({\rm{D\hat EC}} = \frac{{180^\circ - 85.5^\circ }}{3}\) (M1)
\({\rm{D\hat EC}} = 31.5^\circ \) (A1)(G2)
(ii) \(\frac{{\sin (31.5^\circ )}}{9} = \frac{{\sin (85.5^\circ )}}{{{\text{DE}}}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted sine rule, (A1) for correct substitution.
\({\text{DE}} = 17.2{\text{ (km)}}(17.1718 \ldots )\). (A1)(ft)(G2)
\(0.5 \times 17.1718 \ldots \times 9 \times \sin (63^\circ )\) (A1)(ft)(M1)(A1)(ft)
Note: Award (A1)(ft) for \(63\) seen, (M1) for substituted triangle area formula, (A1)(ft) for \(0.5 \times 17.1718 \ldots \times 9 \times \sin ({\text{their angle CDE}})\).
OR
\({\text{(triangle height}} = ){\text{ }}9 \times \sin (63^\circ )\) (A1)(ft)(A1)(ft)
\({\text{0.5}} \times {\text{17.1718}} \ldots \times {\text{9}} \times {\text{sin(their angle CDE)}}\) (M1)
Note: Award (A1)(ft) for \(63\) seen, (A1)(ft) for correct triangle height with their angle \({\text{CDE}}\), (M1) for \({\text{0.5}} \times {\text{17.1718}} \ldots \times {\text{9}} \times {\text{sin(their angle CDE)}}\).
\( = 68.9{\text{ k}}{{\text{m}}^2}\;\;\;(68.8509 \ldots )\) (A1)(ft)(G3)
Notes: Units are required for the last (A1)(ft) mark to be awarded.
Follow through from parts (b)(i) and (b)(ii).
Follow through from their angle \({\text{CDE}}\) within this part of the question.

