| Date | May 2017 | Marks available | 3 | Reference code | 17M.1.sl.TZ1.13 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 13 | Adapted from | N/A |
Question
A triangular postage stamp, ABC, is shown in the diagram below, such that \({\text{AB}} = 5{\text{ cm}},{\rm{ B\hat AC}} = 34^\circ ,{\rm{ A\hat BC}} = 26^\circ \) and \({\rm{A\hat CB}} = 120^\circ \).
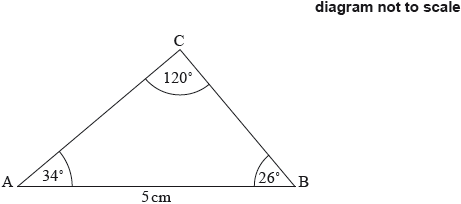
Find the length of BC.
Find the area of the postage stamp.
Markscheme
\(\frac{{{\text{BC}}}}{{\sin 34^\circ }} = \frac{5}{{\sin 120^\circ }}\) (M1)(A1)
Note: Award (M1) for substituted sine rule formula, (A1) for correct substitutions.
\({\text{BC}} = 3.23{\text{ (cm) }}\left( {3.22850 \ldots {\text{ (cm)}}} \right)\) (A1) (C3)
[3 marks]
\(\frac{1}{2}(5)(3.22850)\sin 26^\circ \) (M1)(A1)(ft)
Note: Award (M1) for substituted area of a triangle formula, (A1) for correct substitutions.
\( = 3.54{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}\left( {3.53820 \ldots {\text{ }}({\text{c}}{{\text{m}}^2})} \right)\) (A1)(ft) (C3)
Note: Follow through from part (a).
[3 marks]
Examiners report
Syllabus sections
- 17N.2.sl.TZ0.3d.ii: Find the percentage error in Abdallah’s estimate.
- 17N.2.sl.TZ0.3d.i: Calculate Abdallah’s estimate for the area.
- 17N.2.sl.TZ0.3c: Find the area of ABCD.
- 17N.2.sl.TZ0.3b: Calculate angle \({\rm{B\hat CD}}\).
- 17N.2.sl.TZ0.3a: Show that \({\text{BD}} = 93{\text{ m}}\) correct to the nearest metre.
- 17N.1.sl.TZ0.10c: Find the vertical height of B above the ground.
- 17N.1.sl.TZ0.10b: Write down the angle of elevation of B from E.
- 17N.1.sl.TZ0.10a: Find the length of EB.
- 18M.2.sl.TZ2.5c: Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is...
- 18M.2.sl.TZ2.5b: Find the percentage error on Giovanni’s diagram.
- 18M.2.sl.TZ2.5a.iii: Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
- 18M.2.sl.TZ2.5a.ii: Use Giovanni's diagram to calculate the length of AX.
- 18M.2.sl.TZ2.5a.i: Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning...
- 18M.1.sl.TZ2.8b: Calculate the area of the park.
- 18M.1.sl.TZ2.8a: Calculate the length of side AC in km.
- 18M.2.sl.TZ1.1f: Calculate the total length of metal required for one support.
- 18M.2.sl.TZ1.1e: Show that Farmer Brown is incorrect.
- 18M.2.sl.TZ1.1d: Calculate the length of AE.
- 18M.2.sl.TZ1.1c: Calculate the length of MN.
- 18M.2.sl.TZ1.1b: Calculate the total volume of the barn.
- 18M.2.sl.TZ1.1a: Calculate the area of triangle EAD.
- 18M.1.sl.TZ1.8c: Find the size of the angle of depression of B from P.
- 18M.1.sl.TZ1.8b: Find the size of angle APB.
- 18M.1.sl.TZ1.8a: On the diagram, draw and label with an x the angle of depression of B from P.
- 17M.2.sl.TZ2.4e: Calculate the total length of the track.
- 17M.2.sl.TZ2.4d: Find the length of the path CE.
- 17M.2.sl.TZ2.4c: Find the area of the park.
- 17M.2.sl.TZ2.4b: Show that angle DBC is 48.7°, correct to three significant figures.
- 17M.2.sl.TZ2.4a: Find the length of the path BD.
- 17M.2.sl.TZ1.2e: Calculate the length of CF.
- 17M.2.sl.TZ1.2d: Find the length of the perimeter of ABCDE.
- 17M.2.sl.TZ1.2c: Show that angle \({\rm{B\hat AE}} = 67.4^\circ \), correct to one decimal place.
- 17M.2.sl.TZ1.2b: Find the length of CD.
- 17M.2.sl.TZ1.2a.ii: Show that the equation in part (a)(i) simplifies to \(3{x^2} + 19x - 414 = 0\).
- 17M.2.sl.TZ1.2a.i: Write down an equation for the area of ABCDE using the above information.
- 17M.1.sl.TZ1.13b: Find the area of the postage stamp.
- 16M.2.sl.TZ2.4f: Calculate the maximum number of cups that can be completely filled with the...
- 16M.2.sl.TZ2.4e: Chavi is celebrating her birthday with her friends on the playground. Her mother brings a...
- 16M.2.sl.TZ2.4d: Chavi estimates that the height of the tree is \(6\,{\text{m}}\). Calculate the percentage...
- 16M.2.sl.TZ2.4c: There is a tree at \({\text{C}}\), perpendicular to the ground. The angle of elevation to the...
- 16M.2.sl.TZ2.4b: Calculate angle \({\text{ADC}}\).
- 16M.2.sl.TZ2.4a: A playground, when viewed from above, is shaped like a quadrilateral, \({\text{ABCD}}\),...
- 16M.1.sl.TZ2.6b: Calculate the area of the Bermuda triangle.
- 16M.1.sl.TZ2.6a: When Bermuda \({\text{(B)}}\), Puerto Rico \({\text{(P)}}\), and Miami \({\text{(M)}}\) are...
- 16M.2.sl.TZ1.4f: Ahmad and his friends like to sit in the pyramid’s shadow, \({\text{ABW}}\), to cool down.At...
- 16M.2.sl.TZ1.4e: Ahmad is a tour guide at the Great Pyramid of Giza. He claims that the amount of stone used...
- 16M.2.sl.TZ1.4d: Write down your answer to part (c) in the form \(a \times {10^k}\) where...
- 16M.2.sl.TZ1.4c: Find the volume of the pyramid.
- 16M.2.sl.TZ1.4b: Calculate the height of the pyramid, \({\text{VO}}\) .
- 16M.2.sl.TZ1.4a: The Great Pyramid of Giza in Egypt is a right pyramid with a square base. The pyramid is made...
- 16N.2.sl.TZ0.5f: the length of the fence, BP.
- 16N.2.sl.TZ0.5e: the length of AP;
- 16N.2.sl.TZ0.5d: the area of quadrilateral ABCD;
- 16N.2.sl.TZ0.5c: the area of triangle ABD;
- 16N.2.sl.TZ0.5b: the size of angle DAB;
- 16N.2.sl.TZ0.5a: the length of BD;
- 16N.2.sl.TZ0.3f: Write down the length of MD correct to five significant figures.
- 10M.1.sl.TZ1.7b: Calculate the length of BC in cm.
- 10M.2.sl.TZ1.2e: It is known that AC = 5 and BC = 8.06. Calculate the size of angle ACB.
- 10M.2.sl.TZ1.2f: It is known that AC = 5 and BC = 8.06. Calculate the area of triangle ACB.
- 10N.1.sl.TZ0.12b: Find the area of the triangle AOB.
- 10N.2.sl.TZ0.3a: Find the length of the road AB.
- 10N.2.sl.TZ0.3b: Find the size of the angle CAB.
- 12N.2.sl.TZ0.3b: He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle...
- 12N.2.sl.TZ0.3a: Find the length of BC.
- 12N.2.sl.TZ0.3c: He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle...
- 12M.1.sl.TZ1.10b: Calculate the size of angle ACB.
- 12M.1.sl.TZ1.10a: Calculate the length of AC.
- 12M.1.sl.TZ1.13a: Find the length of AC.
- 12M.1.sl.TZ1.13b: Find the area of triangle ABC.
- 10M.2.sl.TZ2.4b.i: Find the length of BC.
- 12M.1.sl.TZ2.7c: The area of triangle ABC is 360 cm2. Calculate the length of side AC. Express your answer in...
- 12M.2.sl.TZ2.4f: Ahmed is at point P , a distance x metres from M on horizontal ground, as shown in the...
- 12M.2.sl.TZ2.4g: Ahmed is at point P , a distance x metres from M on horizontal ground, as shown in the...
- 11N.2.sl.TZ0.3d: Show that the triangle ABC is not right angled.
- 11N.2.sl.TZ0.3a: Calculate the size of angle ADB.
- 11N.2.sl.TZ0.3b: Find the area of triangle ADB.
- 11N.2.sl.TZ0.3c: Calculate the size of angle BCD.
- 09N.2.sl.TZ0.1B, c: Inside the forest a second path forms the three sides of another triangle named ABC. Angle...
- 09N.2.sl.TZ0.1B, a: Calculate the length of the third side of the triangle. Give your answer correct to the...
- 09N.2.sl.TZ0.1B, b: Calculate the area enclosed by the path that goes around the forest.
- 09M.1.sl.TZ1.10a: Calculate the size of angle ACB.
- 09M.2.sl.TZ1.4d: A different chocolate bar made with the same mixture also has the shape of a triangular...
- 11M.2.sl.TZ1.5a: Calculate the length of the fence.
- 11M.2.sl.TZ1.5d: Calculate the area of triangle ABD .
- 09M.2.sl.TZ2.3a: Find the size of BĈA.
- 11M.2.sl.TZ1.5c: Show that the size of angle ABD is \({18.8^ \circ }\) , correct to three significant figures.
- 09M.2.sl.TZ2.3b: Calculate the length of AD.
- 09M.2.sl.TZ2.3e: Calculate the area of the triangle ABD.
- 11M.1.sl.TZ2.10b: Calculate the length of AC.
- 13M.2.sl.TZ1.5b: Calculate the length of AQ.
- 13M.2.sl.TZ1.5e: Find the size of the angle AQC.
- 13M.2.sl.TZ1.5f: Calculate the total area of the glass needed to construct (i) the two rectangular faces of...
- 11M.2.sl.TZ2.4b: Calculate the length of AC.
- 11M.2.sl.TZ2.4c: Calculate the area of the field ABC.
- 13M.1.sl.TZ2.5b: Find the size of angle ADC.
- 13M.1.sl.TZ2.5a: Find the length of AC in centimetres.
- 11M.2.sl.TZ2.4e: A goat is attached to one end of a rope of length 7 m. The other end of the rope is attached...
- 13M.2.sl.TZ2.3b: Calculate the area of the triangle PTS.
- SPM.2.sl.TZ0.2a: Calculate the size of angle ACB.
- SPM.2.sl.TZ0.2b: Calculate the area of the building’s footprint, ABC.
- 07M.2.sl.TZ0.2ii.a: (i) Find the value of angle \({\text{B}}\hat {\rm T}{\text{L}}\). (ii) Use triangle BTL to...
- 07M.2.sl.TZ0.2ii.c: Leonardo now walks to point M, a distance 200 m from B on the opposite side of the tower....
- 07N.1.sl.TZ0.9b: Find the size of angle BAC.
- 07N.2.sl.TZ0.2d: Calculate the angle at the vertex, \({\text{B}}{\operatorname {\hat V}}{\text{C}}\).
- 07N.1.sl.TZ0.9a: Find the distance between A and C.
- 08N.2.sl.TZ0.2b: (i) Write down the size of angle BCA. (ii) Calculate the length of AB.
- 08N.2.sl.TZ0.2c: Show that the area of the sandbox is \(31.1{\text{ }}{{\text{m}}^2}\) correct to 3 s.f.
- 08N.2.sl.TZ0.2a: Find the length of AC.
- 08M.1.sl.TZ1.7b: Calculate the length of \({\text{AB}}\).
- 08M.1.sl.TZ1.7c: Find the area of triangle \({\text{ABC}}\).
- 08M.2.sl.TZ2.3i.b: Find the length of \({\text{AC}}\).
- 08M.2.sl.TZ2.3i.a: Angle \({\text{ABC}}\) is acute. Show that the angle \({\text{ABC}}\) is \({30^ \circ }\).
- 09M.2.sl.TZ1.4a, ii: Hence or otherwise find the area of the triangular end of the chocolate bar.
- 10M.2.sl.TZ1.4a.ii: Sketch the triangle VCA showing clearly the length of VC and the size of angle VCA.
- 10M.2.sl.TZ2.4b.iii: Calculate the area of the lawn.
- 14M.2.sl.TZ2.2c: The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of...
- 14M.2.sl.TZ2.2e: The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of...
- 14M.2.sl.TZ2.2f: The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of...
- 13N.2.sl.TZ0.2b: Calculate the area of triangle \({\text{ABC}}\).
- 13N.2.sl.TZ0.2a: Calculate the length of \({\text{AC}}\).
- 14M.2.sl.TZ1.4b: Find the area of the triangular field.
- 14M.2.sl.TZ1.4c: \({\text{M}}\) is the midpoint of \({\text{AC}}\). Find the length of \({\text{BM}}\).
- 14M.2.sl.TZ1.4a: Find the size of angle \(ABC\).
- 15M.1.sl.TZ2.8c: Find the length of \({\rm{CB}}\).
- 15M.1.sl.TZ2.12c: Hence, or otherwise, find the area of the triangle \({\text{CAV}}\).
- 15M.2.sl.TZ1.4a: Calculate the total length of the course.
- 15M.2.sl.TZ1.4c: It is estimated that the fastest boat in the race can travel at an average speed of...
- 15M.2.sl.TZ1.4d: To comply with safety regulations, the area inside the triangular course must be kept clear...
- 14N.2.sl.TZ0.4c: Calculate the area of triangle \({\text{DEC}}\).
- 14N.2.sl.TZ0.4a: (i) Find the size of angle \({\rm{ACB}}\). (ii) Show that the size of angle...
- 14N.2.sl.TZ0.4b: The surveyor measures the size of angle \({\text{CDE}}\) to be twice that of angle...

