| Date | May 2014 | Marks available | 3 | Reference code | 14M.2.sl.TZ2.2 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
A cross-country running course consists of a beach section and a forest section. Competitors run from \({\text{A}}\) to \({\text{B}}\), then from \({\text{B}}\) to \({\text{C}}\) and from \({\text{C}}\) back to \({\text{A}}\).
The running course from \({\text{A}}\) to \({\text{B}}\) is along the beach, while the course from \({\text{B}}\), through \({\text{C}}\) and back to \({\text{A}}\), is through the forest.
The course is shown on the following diagram.
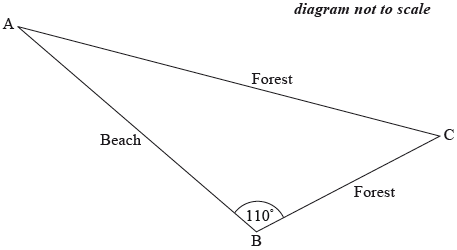
Angle \({\text{ABC}}\) is \(110^\circ\).
It takes Sarah \(5\) minutes and \(20\) seconds to run from \({\text{A}}\) to \({\text{B}}\) at a speed of \(3.8{\text{ m}}{{\text{s}}^{ - 1}}\).
Using ‘distance = speed \( \times \) time’, show that the distance from \({\text{A}}\) to \({\text{B}}\) is \(1220\) metres correct to 3 significant figures.
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the speed, in \({\text{m}}{{\text{s}}^{ - 1}}\), that Sarah runs from \({\text{B}}\) to \({\text{C}}\).
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the distance, in metres, from \({\mathbf{C}}\) to \({\mathbf{A}}\).
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the total distance, in metres, of the cross-country running course.
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Find the size of angle \({\text{BCA}}\).
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the area of the cross-country course bounded by the lines \({\text{AB}}\), \({\text{BC}}\) and \({\text{CA}}\).
Markscheme
\(3.8 \times 320\) (A1)
Note: Award (A1) for \(320\) or equivalent seen.
\( = 1216\) (A1)
\( = 1220{\text{ (m)}}\) (AG)
Note: Both unrounded and rounded answer must be seen for the final (A1) to be awarded.
[2 marks]
\(\frac{{850}}{{303}}{\text{ (m}}{{\text{s}}^{ - 1}}){\text{ (2.81, 2.80528}} \ldots {\text{)}}\) (A1)(G1)
[1 mark]
\({\text{A}}{{\text{C}}^2} = {1220^2} + {850^2} - 2(1220)(850)\cos 110^\circ \) (M1)(A1)
Note: Award (M1) for substitution into cosine rule formula, (A1) for correct substitutions.
\({\text{AC}} = 1710{\text{ (m) (1708.87}} \ldots {\text{)}}\) (A1)(G2)
Notes: Accept \(1705{\text{ }} (1705.33…)\).
[3 marks]
\(1220 + 850 + {\text{1708.87}} \ldots \) (M1)
\( = {\text{3780 (m) (3778.87}} \ldots {\text{)}}\) (A1)(ft)(G1)
Notes: Award (M1) for adding the three sides. Follow through from their answer to part (c). Accept \(3771{\text{ }} (3771.33…)\).
[2 marks]
\(\frac{{\sin C}}{{1220}} = \frac{{\sin 110^\circ }}{{{\text{1708.87}} \ldots }}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into sine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.9^{\circ}, 42.0^{\circ}, 42.2^{\circ}, 42.3^{\circ}\).
OR
\(\cos C = \frac{{{\text{1708.87}}{ \ldots ^2} + {{850}^2} - {{1220}^2}}}{{2 \times {\text{1708.87}} \ldots \times 850}}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into cosine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.2^{\circ}, 41.8^{\circ}, 42.4^{\circ}\).
[3 marks]
\(\frac{1}{2} \times 1220 \times 850 \times \sin 110^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times {\text{1708.87}} \ldots \times 850 \times \sin {\text{42.1339}} \ldots ^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times 1220 \times {\text{1708.87}} \ldots \times \sin {\text{27.8661}} \ldots ^\circ \) (M1)(A1)(ft)
Note: Award (M1) for substitution into area formula, (A1)(ft) for correct substitution.
\( = 487\,000{\text{ }}{{\text{m}}^2}{\text{ (487}}\,{\text{230}} \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G2)
Notes: The answer is \(487\,000{\text{ }}{{\text{m}}^2}\), units are required.
Accept \(486\,000{\text{ }}{{\text{m}}^2}{\text{ (485}}\,{\text{633}} \ldots {\text{ }}{{\text{m}}^2})\).
If workings are not shown and units omitted, award (G1) for \(487\,000{\text{ or }}486\,000\).
Follow through from parts (c) and (e).
[3 marks]

