| Date | May 2014 | Marks available | 4 | Reference code | 14M.2.sl.TZ1.4 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
ABC is a triangular field on horizontal ground. The lengths of AB and AC are 70 m and 50 m respectively. The size of angle BCA is 78°.
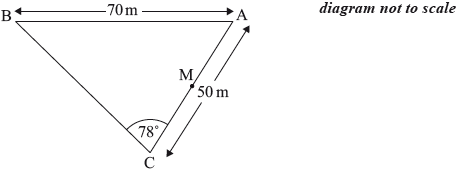
Find the size of angle \(ABC\).
Find the area of the triangular field.
\({\text{M}}\) is the midpoint of \({\text{AC}}\).
Find the length of \({\text{BM}}\).
A vertical mobile phone mast, \({\text{TB}}\), is built next to the field with its base at \({\text{B}}\). The angle of elevation of \({\text{T}}\) from \({\text{M}}\) is \(63.4^\circ \). \({\text{N}}\) is the midpoint of the mast.
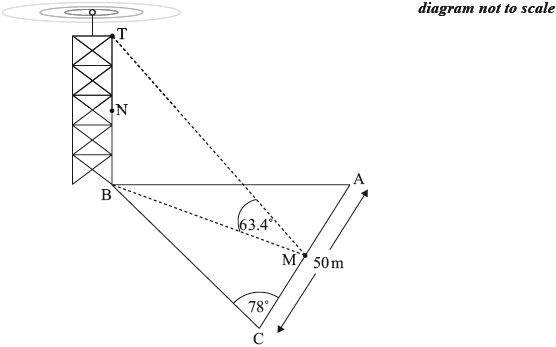
Calculate the angle of elevation of \({\text{N}}\) from \({\text{M}}\).
Markscheme
\(\frac{{70}}{{\sin 78}} = \frac{{50}}{{\sin {\rm{A\hat BC}}}}\) (M1)(A1)
Note: Award (M1) for substituted sine rule, (A1) for correct substitution.
\({\rm{A\hat BC}} = 44.3^\circ \) (\(44.3209...\)) (A1)(G3)
Note: If radians are used the answer is \(0.375918...\), award at most (M1)(A1)(A0).
[3 marks]
\({\text{area }}\Delta {\text{ABC}} = \frac{1}{2} \times 70 \times 50 \times \sin (57.6790 \ldots )\) (A1)(M1)(A1)(ft)
Notes: Award (A1)(ft) for their \(57.6790…\) seen, (M1) for substituted area formula, (A1)(ft) for correct substitution.
Follow through from part (a).
\( = 1480{\text{ }}{{\text{m}}^2}\) \((1478.86 \ldots )\) (A1)(ft)(G3)
Notes: The answer is \(1480{\text{ }}{{\text{m}}^2}\), units are required. \(1479.20…\) if 3 sf used.
If radians are used the answer is \(1554.11 \ldots {{\text{m}}^2}\), award (A1)(ft)(M1)(A1)(ft)(A1)(ft)(G3).
[4 marks]
\({\text{B}}{{\text{M}}^2} = {70^2} + {25^2} - 2 \times 70 \times 25 \times \cos (57.6790 \ldots )\) (M1)(A1)(ft)
Notes: Award (M1) for substituted cosine rule, (A1)(ft) for correct substitution. Follow through from their angle in part (b).
\({\text{BM}} = 60.4{\text{ (m)}}\) \((60.4457 \ldots )\) (A1)(ft)(G2)
Notes: If the 3 sf answer is used the answer is \(60.5{\text{ }}({\text{m}})\).
If radians are used the answer is \(62.5757… {\text{ }} ({\text{m}})\), award (M1)(A1)(ft)(A1)(ft)(G2).
[3 marks]
\(\tan 63.4^\circ = \frac{{{\text{TB}}}}{{60.4457 \ldots }}\) (M1)
Note: Award (M1) for their correctly substituted trig equation.
\({\text{TB}} = 120.707 \ldots \) (A1)(ft)
Notes: Follow through from part (c). If 3 sf answers are used throughout, \({\text{TB}} = 120.815 \ldots \)
If \({\text{TB}} = 120.707 \ldots \) is seen without working, award (A2).
\(\tan {\rm{N\hat MB = }}\frac{{\left( {\frac{{120.707 \ldots }}{2}} \right)}}{{60.4457 \ldots }}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for their \({\text{TB}}\) divided by \(2\) seen, (M1) for their correctly substituted trig equation.
Follow through from part (c) and within part (d).
\({\rm{N\hat MB = 45.0^\circ }}\) \({\text{(44.9563}} \ldots {\text{)}}\) (A1)(ft)(G3)
Notes: If 3 sf are used throughout, answer is \(45^\circ \).
If radians are used the answer is \(0.308958…\), and if full working is shown, award at most (M1)(A1)(ft)(A1)(ft)(M1)(A0).
If no working is shown for radians answer, award (G2).
OR
\(\tan {\rm{N\hat MB}} = \frac{{{\text{NB}}}}{{{\text{BM}}}}\) (M1)
\(\tan 63.4^\circ = \frac{{2 \times {\text{NB}}}}{{{\text{BM}}}}\) (A1)(M1)
Note: Award (A1) for \(2 \times {\text{NB}}\) seen.
\(\tan {\rm{N\hat MB}} = \frac{1}{2}\tan 63.4^\circ \) (M1)
\({\rm{N\hat MB}} = 45.0^\circ \) \((44.9563 \ldots )\) (A1)(G3)
Notes: If radians are used the answer is \(0.308958…\), and if full working is shown, award at most (M1)(A1)(M1)(M1)(A0). If no working is shown for radians answer, award (G2).
[5 marks]

