| Date | May 2015 | Marks available | 3 | Reference code | 15M.1.sl.TZ2.12 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Hence or otherwise | Question number | 12 | Adapted from | N/A |
Question
In the following diagram, ABCD is the square base of a right pyramid with vertex V. The centre of the base is O. The diagonal of the base, AC, is 8 cm long. The sloping edges are 10 cm long.
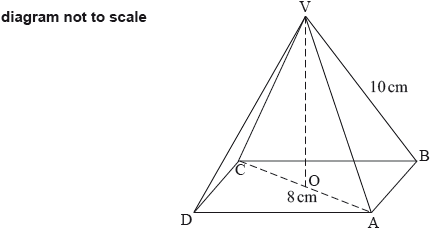
Write down the length of \({\text{AO}}\).
Find the size of the angle that the sloping edge \({\text{VA}}\) makes with the base of the pyramid.
Hence, or otherwise, find the area of the triangle \({\text{CAV}}\).
Markscheme
\({\text{AO}} = 4{\text{ (cm)}}\) (A1) (C1)
\(\cos {\rm{O\hat AV}} = \frac{4}{{10}}\) (M1)
Note: Award (M1) for their correct trigonometric ratio.
OR
\(\cos {\rm{O\hat AV}} = \frac{{{{10}^2} + {8^2} - {{10}^2}}}{{2 \times 10 \times 8}}\;\;\;\)OR\(\;\;\;\frac{{{{10}^2} + {4^2} - {{(9.16515 \ldots )}^2}}}{{2 \times 10 \times 4}}\) (M1)
Note: Award (M1) for correct substitution into the cosine rule formula.
\({\rm{O\hat AV}} = 66.4^\circ \;\;\;(66.4218 \ldots )\) (A1)(ft) (C2)
Notes: Follow through from their answer to part (a).
\({\text{area}} = \frac{{8 \times 10 \times \sin (66.4218 \ldots ^\circ)}}{2}\;\;\;\)OR\(\;\;\;\frac{1}{2} \times 8 \times \sqrt {{{10}^2} - {4^{\text{2}}}} \)
OR\(\;\;\;\frac{1}{2} \times 10 \times 10 \times \sin (47.1563 \ldots ^\circ )\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into the area formula, (A1)(ft) for correct substitutions. Follow through from their answer to part (b) and/or part (a).
\({\text{area}} = 36.7{\text{ c}}{{\text{m}}^2}\;\;\;(36.6606 \ldots {\text{ c}}{{\text{m}}^2})\) (A1)(ft) (C3)
Notes: Accept an answer of \(8\sqrt {21} {\text{ c}}{{\text{m}}^2}\) which is the exact answer.

