| Date | November 2013 | Marks available | 3 | Reference code | 13N.2.sl.TZ0.2 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Calculate | Question number | 2 | Adapted from | N/A |
Question
A manufacturer has a contract to make \(2600\) solid blocks of wood. Each block is in the shape of a right triangular prism, \({\text{ABCDEF}}\), as shown in the diagram.
\({\text{AB}} = 30{\text{ cm}},{\text{ BC}} = 24{\text{ cm}},{\text{ CD}} = 25{\text{ cm}}\) and angle \({\rm{A\hat BC}} = 35^\circ {\text{ }}\).
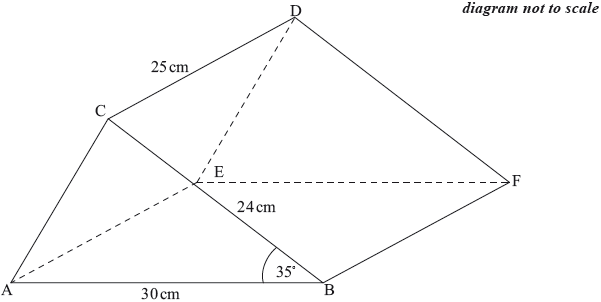
Calculate the length of \({\text{AC}}\).
Calculate the area of triangle \({\text{ABC}}\).
Assuming that no wood is wasted, show that the volume of wood required to make all \(2600\) blocks is \({\text{13}}\,{\text{400}}\,{\text{000 c}}{{\text{m}}^3}\), correct to three significant figures.
Write \({\text{13}}\,{\text{400}}\,{\text{000}}\) in the form \(a \times {10^k}\) where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\).
Show that the total surface area of one block is \({\text{2190 c}}{{\text{m}}^2}\), correct to three significant figures.
The blocks are to be painted. One litre of paint will cover \(22{\text{ }}{{\text{m}}^2}\).
Calculate the number of litres required to paint all \(2600\) blocks.
Markscheme
\({\text{A}}{{\text{C}}^2} = {30^2} + {24^2} - 2 \times 30 \times 24 \times \cos 35^\circ \) (M1)(A1)
Note: Award (M1) for substituted cosine rule formula,
(A1) for correct substitutions.
\({\text{AC}} = 17.2{\text{ cm}}\) \((17.2168…)\) (A1)(G2)
Notes: Use of radians gives \(52.7002…\) Award (M1)(A1)(A0).
No marks awarded in this part of the question where candidates assume that angle \({\text{ACB}} = 90^\circ \).
[3 marks]
Units are required in part (b).
Area of triangle \({\text{ABC = }}\frac{1}{2} \times 24 \times 30 \times \sin 35^\circ \) (M1)(A1)
Notes: Award (M1) for substitution into area formula, (A1) for correct substitutions.
Special Case: Where a candidate has assumed that angle \({\text{ACB}} = 90^\circ \) in part (a), award (M1)(A1) for a correct alternative substituted formula for the area of the triangle \(\left( {ie{\text{ }}\frac{1}{2} \times {\text{base}} \times {\text{height}}} \right)\).
\( = 206{\text{ c}}{{\text{m}}^2}\) \((206.487 \ldots {\text{c}}{{\text{m}}^2})\) (A1)(G2)
Notes: Use of radians gives negative answer, \(–154.145…\) Award (M1)(A1)(A0).
Special Case: Award (A1)(ft) where the candidate has arrived at an area which is correct to the standard rounding rules from their lengths (units required).
[3 marks]
\(206.487… \times 25 \times 2600\) (M1)
Note: Award (M1) for multiplication of their answer to part (b) by \(25\) and \(2600\).
\({\text{13}}\,{\text{421}}\,{\text{688.61}}\) (A1)
Note: Accept unrounded answer of \({\text{13}}\,{\text{390}}\,{\text{000}}\) for use of \(206\).
\({\text{13}}\,{\text{400}}\,{\text{000}}\) (AG)
Note: The final (A1) cannot be awarded unless both the unrounded and rounded answers are seen.
[2 marks]
\(1.34 \times {10^7}\) (A2)
Notes: Award (A2) for the correct answer.
Award (A1)(A0) for \(1.34\) and an incorrect index value.
Award (A0)(A0) for any other combination (including answers such as \(13.4 \times {10^6}\)).
[2 marks]
\(2 \times 206.487 \ldots + 24 \times 25 + 30 \times 25 + 17.2168 \ldots \times 25\) (M1)(M1)
Note: Award (M1) for multiplication of their answer to part (b) by \(2\) for area of two triangular ends, (M1) for three correct rectangle areas using \(24\), \(30\) and their \(17.2\).
\(2193.26…\) (A1)
Note: Accept \(2192\) for use of 3 sf answers.
\(2190\) (AG)
Note: The final (A1) cannot be awarded unless both the unrounded and rounded answers are seen.
[3 marks]
\(\frac{{2190 \times 2600}}{{22 \times 10\,000}}\) (M1)(M1)
Notes: Award (M1) for multiplication by \(2600\) and division by \(22\), (M1) for division by \({10\,000}\).
The use of \(22\) may be implied ie division by \(2200\) would be acceptable.
\(25.9\) litres \((25.8818…)\) (A1)(G2)
Note: Accept \(26\).
[3 marks]
Examiners report
Some candidates assumed that triangle ACB was a right angled triangle with angle \({\text{ACB}} = 90^\circ \). Such candidates earned no marks for part (a) but were able to recover most of the marks in the remainder of the question. For those candidates who correctly used the cosine rule for part (a), most achieved all 3 marks for this part and used a correct formula for the area of the triangle in part (b) to obtain at least 2 marks for this part. The final mark was not awarded, however, if no units or the incorrect units were given. Parts (c) and (e) were generally well done with many candidates showing the unrounded answer before the required answer. Part (f) proved to be quite problematic for many candidates. Whilst many were able to earn a method mark for \(\frac{{2190 \times 2600}}{{22}}\), a significant number of these candidates were unable to convert the units correctly and very few correct answers were seen. Indeed, the most popular answer seemed to be 2590 litres.
Some candidates assumed that triangle ACB was a right angled triangle with angle \({\text{ACB}} = 90^\circ \). Such candidates earned no marks for part (a) but were able to recover most of the marks in the remainder of the question. For those candidates who correctly used the cosine rule for part (a), most achieved all 3 marks for this part and used a correct formula for the area of the triangle in part (b) to obtain at least 2 marks for this part. The final mark was not awarded, however, if no units or the incorrect units were given. Parts (c) and (e) were generally well done with many candidates showing the unrounded answer before the required answer. Part (f) proved to be quite problematic for many candidates. Whilst many were able to earn a method mark for \(\frac{{2190 \times 2600}}{{22}}\), a significant number of these candidates were unable to convert the units correctly and very few correct answers were seen. Indeed, the most popular answer seemed to be 2590 litres.
Some candidates assumed that triangle ACB was a right angled triangle with angle \({\text{ACB}} = 90^\circ \). Such candidates earned no marks for part (a) but were able to recover most of the marks in the remainder of the question. For those candidates who correctly used the cosine rule for part (a), most achieved all 3 marks for this part and used a correct formula for the area of the triangle in part (b) to obtain at least 2 marks for this part. The final mark was not awarded, however, if no units or the incorrect units were given. Parts (c) and (e) were generally well done with many candidates showing the unrounded answer before the required answer. Part (f) proved to be quite problematic for many candidates. Whilst many were able to earn a method mark for \(\frac{{2190 \times 2600}}{{22}}\), a significant number of these candidates were unable to convert the units correctly and very few correct answers were seen. Indeed, the most popular answer seemed to be 2590 litres.
Some candidates assumed that triangle ACB was a right angled triangle with angle \({\text{ACB}} = 90^\circ \). Such candidates earned no marks for part (a) but were able to recover most of the marks in the remainder of the question. For those candidates who correctly used the cosine rule for part (a), most achieved all 3 marks for this part and used a correct formula for the area of the triangle in part (b) to obtain at least 2 marks for this part. The final mark was not awarded, however, if no units or the incorrect units were given. Parts (c) and (e) were generally well done with many candidates showing the unrounded answer before the required answer. Part (f) proved to be quite problematic for many candidates. Whilst many were able to earn a method mark for \(\frac{{2190 \times 2600}}{{22}}\), a significant number of these candidates were unable to convert the units correctly and very few correct answers were seen. Indeed, the most popular answer seemed to be 2590 litres.
Some candidates assumed that triangle ACB was a right angled triangle with angle \({\text{ACB}} = 90^\circ \). Such candidates earned no marks for part (a) but were able to recover most of the marks in the remainder of the question. For those candidates who correctly used the cosine rule for part (a), most achieved all 3 marks for this part and used a correct formula for the area of the triangle in part (b) to obtain at least 2 marks for this part. The final mark was not awarded, however, if no units or the incorrect units were given. Parts (c) and (e) were generally well done with many candidates showing the unrounded answer before the required answer. Part (f) proved to be quite problematic for many candidates. Whilst many were able to earn a method mark for \(\frac{{2190 \times 2600}}{{22}}\), a significant number of these candidates were unable to convert the units correctly and very few correct answers were seen. Indeed, the most popular answer seemed to be 2590 litres.
Some candidates assumed that triangle ACB was a right angled triangle with angle \({\text{ACB}} = 90^\circ \). Such candidates earned no marks for part (a) but were able to recover most of the marks in the remainder of the question. For those candidates who correctly used the cosine rule for part (a), most achieved all 3 marks for this part and used a correct formula for the area of the triangle in part (b) to obtain at least 2 marks for this part. The final mark was not awarded, however, if no units or the incorrect units were given. Parts (c) and (e) were generally well done with many candidates showing the unrounded answer before the required answer. Part (f) proved to be quite problematic for many candidates. Whilst many were able to earn a method mark for \(\frac{{2190 \times 2600}}{{22}}\), a significant number of these candidates were unable to convert the units correctly and very few correct answers were seen. Indeed, the most popular answer seemed to be 2590 litres.

