| Date | November 2016 | Marks available | 3 | Reference code | 16N.2.sl.TZ0.5 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Calculate | Question number | 5 | Adapted from | N/A |
Question
A farmer owns a plot of land in the shape of a quadrilateral ABCD.
\({\text{AB}} = 105{\text{ m, BC}} = 95{\text{ m, CD}} = 40{\text{ m, DA}} = 70{\text{ m}}\) and angle \({\text{DCB}} = 90^\circ \).
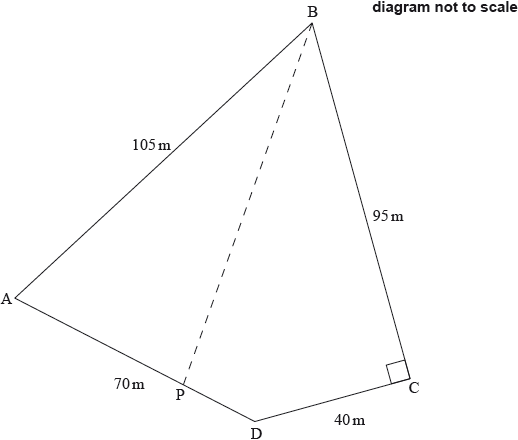
The farmer wants to divide the land into two equal areas. He builds a fence in a straight line from point B to point P on AD, so that the area of PAB is equal to the area of PBCD.
Calculate
the length of BD;
the size of angle DAB;
the area of triangle ABD;
the area of quadrilateral ABCD;
the length of AP;
the length of the fence, BP.
Markscheme
\(({\text{BD}} = ){\text{ }}\sqrt {{{95}^2} + {{40}^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ theorem.
\( = 103{\text{ }}({\text{m}}){\text{ }}\left( {103.077 \ldots ,{\text{ }}25\sqrt {17} } \right)\) (A1)(G2)
[2 marks]
\(\cos {\rm{B\hat AD}} = \frac{{{{105}^2} + {{70}^2} - {{(103.077 \ldots )}^2}}}{{2 \times 105 \times 70}}\) (M1)(A1)(ft)
Note: Award (M1) for substitution into cosine rule, (A1)(ft) for their correct substitutions. Follow through from part (a).
\(({\rm{B\hat AD}}) = 68.9^\circ {\text{ }}(68.8663 \ldots )\) (A1)(ft)(G2)
Note: If their 103 used, the answer is \(68.7995 \ldots \)
[3 marks]
\(({\text{Area of ABD}} = )\frac{1}{2} \times 105 \times 70 \times \sin (68.8663 \ldots )\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into the trig form of the area of a triangle formula.
Award (A1)(ft) for their correct substitutions.
Follow through from part (b).
If 68.8° is used the area \( = 3426.28 \ldots {\text{ }}{{\text{m}}^2}\).
\( = 3430{\text{ }}{{\text{m}}^2}{\text{ }}(3427.82 \ldots )\) (A1)(ft)(G2)
[3 marks]
\({\text{area of ABCD}} = \frac{1}{2} \times 40 \times 95 + 3427.82 \ldots \) (M1)
Note: Award (M1) for correctly substituted area of triangle formula added to their answer to part (c).
\( = 5330{\text{ }}{{\text{m}}^2}{\text{ }}(5327.83 \ldots )\) (A1)(ft)(G2)
[2 marks]
\(\frac{1}{2} \times 105 \times {\text{AP}} \times \sin (68.8663 \ldots ) = 0.5 \times 5327.82 \ldots \) (M1)(M1)
Notes: Award (M1) for the correct substitution into triangle formula.
Award (M1) for equating their triangle area to half their part (d).
\(({\text{AP}} = ){\text{ }}54.4{\text{ }}({\text{m}}){\text{ }}(54.4000 \ldots )\) (A1)(ft)(G2)
Notes: Follow through from parts (b) and (d).
[3 marks]
\({\text{B}}{{\text{P}}^2} = {105^2} + {(54.4000 \ldots )^2} - 2 \times 105 \times (54.4000 \ldots ) \times \cos (68.8663 \ldots )\) (M1)(A1)(ft)
Notes: Award (M1) for substituted cosine rule formula.
Award (A1)(ft) for their correct substitutions. Accept the exact fraction \(\frac{{53}}{{147}}\) in place of \(\cos (68.8663 \ldots )\).
Follow through from parts (b) and (e).
\(({\text{BP}} = ){\text{ }}99.3{\text{ }}({\text{m}}){\text{ }}(99.3252 \ldots )\) (A1)(ft)(G2)
Notes: If 54.4 and \(\cos (68.9)\) are used the answer is \(99.3567 \ldots \)
[3 marks]

