| Date | November 2017 | Marks available | 2 | Reference code | 17N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Emily’s kite ABCD is hanging in a tree. The plane ABCDE is vertical.
Emily stands at point E at some distance from the tree, such that EAD is a straight line and angle BED = 7°. Emily knows BD = 1.2 metres and angle BDA = 53°, as shown in the diagram
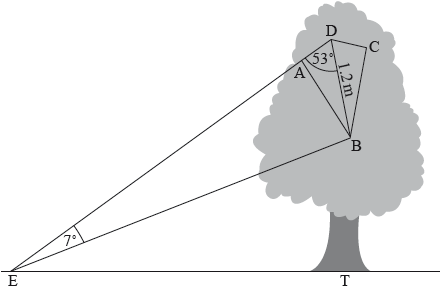
T is a point at the base of the tree. ET is a horizontal line. The angle of elevation of A from E is 41°.
Find the length of EB.
Write down the angle of elevation of B from E.
Find the vertical height of B above the ground.
Markscheme
Units are required in parts (a) and (c).
\(\frac{{{\text{EB}}}}{{\sin 53{\rm{^\circ }}}} = \frac{{1.2}}{{\sin 7{\rm{^\circ }}}}\) (M1)(A1)
Note: Award (M1) for substitution into sine formula, (A1) for correct substitution.
\(({\text{EB}} = ){\text{ }}7.86{\text{ m}}\)\(\,\,\,\)OR\(\,\,\,\)\(786{\text{ cm }}(7.86385 \ldots {\text{ m}}\)\(\,\,\,\)OR\(\,\,\,\)\(786.385 \ldots {\text{ cm}})\) (A1) (C3)
[3 marks]
34° (A1) (C1)
[1 mark]
Units are required in parts (a) and (c).
\(\sin 34^\circ = \frac{{{\text{height}}}}{{7.86385 \ldots }}\) (M1)
Note: Award (M1) for correct substitution into a trigonometric ratio.
\(({\text{height}} = ){\text{ }}4.40{\text{ m}}\)\(\,\,\,\)OR\(\,\,\,\)\(440{\text{ cm }}(4.39741 \ldots {\text{ m}}\)\(\,\,\,\)OR\(\,\,\,\)\(439.741 \ldots {\text{ cm}})\) (A1)(ft) (C2)
Note: Accept “BT” used for height. Follow through from parts (a) and (b). Use of 7.86 gives an answer of 4.39525….
[2 marks]

