| Date | November 2017 | Marks available | 2 | Reference code | 17N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Calculate | Question number | 3 | Adapted from | N/A |
Question
Abdallah owns a plot of land, near the river Nile, in the form of a quadrilateral ABCD.
The lengths of the sides are \({\text{AB}} = {\text{40 m, BC}} = {\text{115 m, CD}} = {\text{60 m, AD}} = {\text{84 m}}\) and angle \({\rm{B\hat AD}} = 90^\circ \).
This information is shown on the diagram.
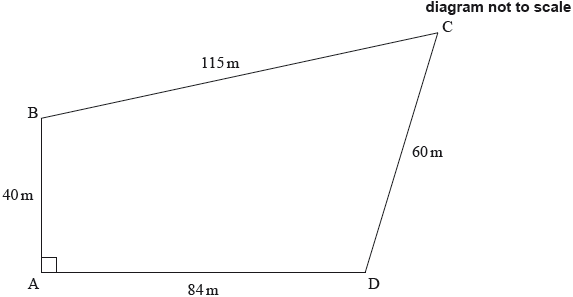
The formula that the ancient Egyptians used to estimate the area of a quadrilateral ABCD is
\({\text{area}} = \frac{{({\text{AB}} + {\text{CD}})({\text{AD}} + {\text{BC}})}}{4}\).
Abdallah uses this formula to estimate the area of his plot of land.
Show that \({\text{BD}} = 93{\text{ m}}\) correct to the nearest metre.
Calculate angle \({\rm{B\hat CD}}\).
Find the area of ABCD.
Calculate Abdallah’s estimate for the area.
Find the percentage error in Abdallah’s estimate.
Markscheme
\({\text{B}}{{\text{D}}^2} = {40^2} + {84^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras.
Accept correct substitution into cosine rule.
\({\text{BD}} = 93.0376 \ldots \) (A1)
\( = 93\) (AG)
Note: Both the rounded and unrounded value must be seen for the (A1) to be awarded.
[2 marks]
\(\cos C = \frac{{{{115}^2} + {{60}^2} - {{93}^2}}}{{2 \times 115 \times 60}}{\text{ }}({93^2} = {115^2} + {60^2} - 2 \times 115 \times 60 \times \cos C)\) (M1)(A1)
Note: Award (M1) for substitution into cosine formula, (A1) for correct substitutions.
\( = 53.7^\circ {\text{ }}(53.6679 \ldots ^\circ )\) (A1)(G2)
[3 marks]
\(\frac{1}{2}(40)(84) + \frac{1}{2}(115)(60)\sin (53.6679 \ldots )\) (M1)(M1)(A1)(ft)
Note: Award (M1) for correct substitution into right-angle triangle area. Award (M1) for substitution into area of triangle formula and (A1)(ft) for correct substitution.
\( = 4460{\text{ }}{{\text{m}}^2}{\text{ }}(4459.30 \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G3)
Notes: Follow through from part (b).
[4 marks]
\(\frac{{(40 + 60)(84 + 115)}}{4}\) (M1)
Note: Award (M1) for correct substitution in the area formula used by ‘Ancient Egyptians’.
\( = 4980{\text{ }}{{\text{m}}^2}{\text{ }}(4975{\text{ }}{{\text{m}}^2})\) (A1)(G2)
[2 marks]
\(\left| {\frac{{4975 - 4459.30 \ldots }}{{4459.30 \ldots }}} \right| \times 100\) (M1)
Notes: Award (M1) for correct substitution into percentage error formula.
\( = 11.6{\text{ }}(\% ){\text{ }}(11.5645 \ldots )\) (A1)(ft)(G2)
Notes: Follow through from parts (c) and (d)(i).
[2 marks]

