| Date | November 2016 | Marks available | 2 | Reference code | 16N.1.sl.TZ0.12 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Complete | Question number | 12 | Adapted from | N/A |
Question
On a work day, the probability that Mr Van Winkel wakes up early is \(\frac{4}{5}\).
If he wakes up early, the probability that he is on time for work is \(p\).
If he wakes up late, the probability that he is on time for work is \(\frac{1}{4}\).
The probability that Mr Van Winkel arrives on time for work is \(\frac{3}{5}\).
Complete the tree diagram below.
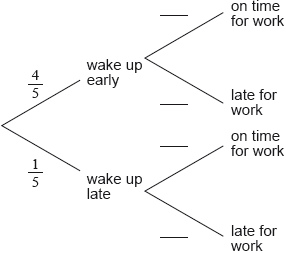
Find the value of \(p\).
Markscheme
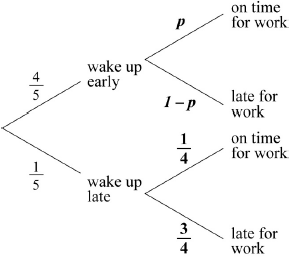 (A1)(A1) (C2)
(A1)(A1) (C2)
Note: Award (A1) for each correct pair of probabilities.
[2 marks]
\(\frac{4}{5}p + \frac{1}{5} \times \frac{1}{4} = \frac{3}{5}\) (A1)(ft)(M1)(M1)
Note: Award (A1)(ft) for two correct products from part (a), (M1) for adding their products, (M1) for equating the sum of any two probabilities to \(\frac{3}{5}\).
\((p = ){\text{ }}\frac{{11}}{{16}}{\text{ }}(0.688,{\text{ }}0.6875)\) (A1)(ft) (C4)
Note: Award the final (A1)(ft) only if \(0 \leqslant p \leqslant 1\). Follow through from part (a).
[4 marks]
Examiners report
Syllabus sections
- 10M.1.sl.TZ2.6c: Find the probability that a randomly chosen student from the group likes peanut butter, given...
- 10N.2.sl.TZ0.1A.e: Find the probability that a student had at least two of the three choices for breakfast.
- 12M.2.sl.TZ2.1g: Leanne notices that on windy days, the probability she catches a fish is 0.1 while on...
- 11M.1.sl.TZ2.9b: One female traveller is to be chosen at random from all those interviewed. Find the...
- 13M.2.sl.TZ1.2d: A student is chosen at random from the 100 that were asked above. Find the probability that...
- 13M.1.sl.TZ2.10b: Alan returns the sock to the laundry basket and selects two socks at random. Find the...
- 13M.1.sl.TZ2.10c: Alan returns the socks to the laundry basket and again selects two socks at random. Find the...
- 13M.2.sl.TZ2.1d: Two families are chosen at random from the group of 40 families. Find the probability that...
- 07M.2.sl.TZ0.5ii.c: Two mice are chosen without replacement. Find P (both mice are short-tailed).
- 08N.2.sl.TZ0.3b: Consider the \(200\) drivers surveyed. One driver is chosen at random. Calculate the...
- 08M.2.sl.TZ2.2i.b: Two people are chosen at random from those surveyed. Find the probability that they both...
- 14M.2.sl.TZ2.1a: Find the value of (i) \({\text{A}}\); (ii) \({\text{B}}\); (iii) \({\text{C}}\).
- 14M.1.sl.TZ1.7b: Calculate the probability that it will snow tomorrow.
- 15M.1.sl.TZ1.8c: Aleph and Beth are each going to roll their die once only. Shin says the probability that...
- 15M.2.sl.TZ2.1e: The number of customers that like only mangoes is equal to the number of customers that like...
- 14N.2.sl.TZ0.2d: During the first trial Mike escapes. Given that Mike escaped, find the probability that he...
- 17M.1.sl.TZ1.4b: Determine whether rock-climbing is offered by the school in the fall/autumn trimester.
- 17M.1.sl.TZ2.2b: Complete the Venn diagram using the above information.
- 17M.1.sl.TZ2.2c: Find the number of children who play only football.
- 17N.2.sl.TZ0.4d: Find the probability that this adult is allergic to nuts and the liquid turns blue.
- 18M.2.sl.TZ2.1c.ii: Find the value of y.
- 12M.2.sl.TZ2.1b: Leanne catches a fish. Find the probability that she (i) catches an undersized bream; (ii)...
- 12M.2.sl.TZ2.1d: Leanne notices that on windy days, the probability she catches a fish is 0.1 while on...
- 11N.2.sl.TZ0.2b: Pam believes that the Mathematics course a student chooses is independent of the language in...
- 09N.1.sl.TZ0.9a: Complete the tree diagram below.
- 09N.1.sl.TZ0.14b: Find the probability that a student studies Spanish given that she studies one language only.
- 09M.2.sl.TZ1.2i, a: Copy and complete the tree diagram to represent this information.
- 09M.2.sl.TZ2.1d: A family is chosen at random. Find the probability that they own a cat, given that they own a...
- 09M.1.sl.TZ2.10b: If events A and B are independent, find the value of \({\text{P}} (A\cap B)\).
- 07N.2.sl.TZ0.1i.a: Copy the tree diagram below and fill in all the probabilities, where NL represents not late,...
- 14M.2.sl.TZ2.1c: The conference lasts for two days. Calculate the probability that Tomek wears trousers on...
- 13N.1.sl.TZ0.7b: Find the probability that Ramzi buys a magazine when he travels to work.
- 13N.2.sl.TZ0.3g: Two women from the group are selected at random. Find the probability that both women...
- 15M.1.sl.TZ1.11b: For a different day, also chosen at random, find the probability that Peter cycled to work...
- 14N.2.sl.TZ0.2b: (i) Find the probability that Mike reaches Trap B. (ii) Find the probability that...
- 16M.2.sl.TZ2.1d: Given that the person had used only one type of transport in the last year, find...
- 17M.1.sl.TZ1.2a: Calculate the percentage of the population of Ottawa that speak English but not French.
- 17M.1.sl.TZ1.2b: Calculate the number of people in Ottawa that speak both English and French.
- 17M.1.sl.TZ2.2d: Write down the value of \(n(F)\).
- 17M.1.sl.TZ2.10b.ii: Find the probability that at least one of Francesco’s light bulbs is defective.
- 18M.1.sl.TZ1.10c: Write down the value of \(n\left( {\left( {F \cup H} \right) \cap S'} \right)\).
- 18M.2.sl.TZ1.2f: Write down the probability that this flight arrived on time.
- 18M.2.sl.TZ1.5a: Write down the probability that Ayako avoids the trap in this wall.
- 18M.2.sl.TZ1.5d.ii: A contestant is chosen at random. Find the probability that this contestant fell into a trap.
- 18M.2.sl.TZ2.1a.ii: Write down the value of b.
- 18M.2.sl.TZ2.1b.ii: Use the tree diagram to find the probability that an employee was late for work.
- 10M.1.sl.TZ1.8a: Complete the tree diagram below, showing the appropriate probabilities.
- 10M.1.sl.TZ2.8b: Find \({\text{P}}(A|B)\).
- 10N.1.sl.TZ0.6c: Find the probability that this person is a smoker or is male.
- 11N.1.sl.TZ0.10b: Find the probability that Ju Shen and Ramón choose different coloured discs from the bag.
- 12N.2.sl.TZ0.2e: Two students are chosen at random from the 450 students. Calculate the probability that (i)...
- 12M.2.sl.TZ2.1e: Leanne notices that on windy days, the probability she catches a fish is 0.1 while on...
- 09N.1.sl.TZ0.14a: Draw a Venn diagram in the space below to illustrate this information.
- 09M.1.sl.TZ1.11b: Find the probability that the difference between the two numbers shown on the dice is 1.
- 13M.2.sl.TZ2.1c: A family is chosen at random from the group of 40 families. Find the probability that the...
- 08M.2.sl.TZ1.2i.e: If a student owns an iPod, write down the probability that the student also owns a digital...
- 10M.2.sl.TZ2.1a.iii: Find the probability that both biscuits are plain.
- 10M.2.sl.TZ2.1c.ii: Find the probability that he chooses a biscuit from the red tin given that it is a chocolate...
- 14M.2.sl.TZ2.1b: Calculate the probability that Tomek wears (i) shorts and no tie; (ii) no...
- 16N.2.sl.TZ0.2d: Find the probability that this person (i) went on at most one trip; (ii) went on...
- 16M.1.sl.TZ2.5c: Find the probability that the number shown on the die is even given that the colour shown on...
- 17N.1.sl.TZ0.7b: One of the students who joined the sports club is chosen at random. Find the probability that...
- 17N.2.sl.TZ0.4a: Find the probability that this person is not allergic to nuts.
- 17N.2.sl.TZ0.4f: Find the probability that the tested adult is allergic to nuts given that the liquid turned...
- 17N.2.sl.TZ0.4b: Find the probability that both people chosen are not allergic to nuts.
- 18M.1.sl.TZ1.10a: Complete the Venn diagram using the given information.
- 18M.2.sl.TZ1.2d.i: Write down the χ2 statistic.
- 18M.2.sl.TZ1.5e: 120 contestants attempted this game. Find the expected number of contestants who fell into a...
- 18M.2.sl.TZ2.1a.i: Write down the value of a.
- 10N.1.sl.TZ0.6b: Write down the probability that this person is male given that they are a smoker.
- 12M.1.sl.TZ1.12c: Merryn was not late for the concert the next day. Given that, find the probability that she...
- 10M.2.sl.TZ2.1c.i: Find the probability that he chooses a chocolate biscuit.
- 09N.1.sl.TZ0.9c: Find the probability that Chuck is late for school.
- 11M.1.sl.TZ1.9b: Calculate the probability of rain tomorrow.
- 11M.1.sl.TZ1.9a: Complete the tree diagram below.
- 11M.2.sl.TZ1.2B.c: One of the survey forms was chosen at random, find the probability that the form showed...
- 09M.1.sl.TZ2.10c: If \({\text{P}} (A \cup B) = \frac{7}{13}\), find the value of \({\text{P}} (A \cap B)\).
- 13M.1.sl.TZ1.5b: Find the probability that Tanay has a sandwich for his lunch.
- 07M.2.sl.TZ0.5i.a: One of the dogs is chosen at random. (i) Find P (the dog is grey and has the yellow...
- 08M.2.sl.TZ1.2i.d: If two students are chosen at random, calculate the probability that they both own a cell...
- 08M.2.sl.TZ1.2ii.a: Copy and complete the probability tree diagram below.
- 08M.2.sl.TZ1.2ii.b: Calculate the probability that (i) Kate goes to the cinema and is not late; (ii) the...
- 08M.1.sl.TZ2.14a: Complete the tree diagram below.
- 14M.2.sl.TZ2.1d: The conference lasts for two days. Calculate the probability that Tomek wears trousers on...
- 15M.1.sl.TZ1.11a: On a day chosen at random, Peter walked to work. Write down the probability that he was on...
- 17M.1.sl.TZ2.10b.i: Find the probability that both light bulbs are not defective.
- 18M.2.sl.TZ1.5c: Copy the probability tree diagram and write down the relevant probabilities along the branches.
- 18M.2.sl.TZ1.2h: Two flights are chosen at random from those which were slightly delayed. Find the...
- 18M.2.sl.TZ2.1e: Find \(n\left( {\left( {C \cup B} \right) \cap P'} \right)\).
- 10M.1.sl.TZ1.8b: Find the probability that Maria is late for school.
- 10M.1.sl.TZ2.8c: Decide whether A and B are independent events. Give a reason for your answer.
- 12M.1.sl.TZ1.12a: Complete the tree diagram below.
- 10M.2.sl.TZ2.1b: Copy and complete the tree diagram below.
- 12M.2.sl.TZ1.2h: Two students are chosen at random from the 120 students. Find the probability that (i) both...
- 09M.2.sl.TZ1.2i, d: Given that they do not have pasta, find the probability that Lisa cooked dinner.
- 09M.2.sl.TZ1.2i, b: Find the probability that Lisa cooks dinner and they do not have pasta.
- 11M.2.sl.TZ1.2B.b: One of the survey forms was chosen at random, find the probability that the form showed...
- 09M.1.sl.TZ2.13c: The die is now thrown twice. Calculate the probability that black appears on top both times.
- 07N.2.sl.TZ0.1i.d: Find the probability that Geraldine travelled by train, given that she is late.
- 08M.2.sl.TZ2.2i.a: One person is chosen at random from those surveyed. Find the probability that this...
- 14M.1.sl.TZ1.7a: Using the information given, complete the following tree diagram.
- 14N.2.sl.TZ0.2a: Write down the value of (i) \(p\) ; (ii) \(q\) ; (iii) \(r\).
- 16M.1.sl.TZ2.5b: Find the probability that the number shown on the die is \(1\) or the colour shown on the...
- 16N.2.sl.TZ0.2a: Draw a Venn diagram to represent the given information, using sets labelled \(B\), \(C\) and...
- 16N.2.sl.TZ0.6f: Using your answer to part (e), find the value of \(r\) which minimizes \(A\).
- 17M.1.sl.TZ1.2c: Write down your answer to part (b) in the form \(a \times {10^k}\) where...
- 17M.1.sl.TZ1.4a: Write down the number of sporting activities offered by the school during its school year.
- 17M.1.sl.TZ1.4c.i: Write down the elements of the set \(F \cap W’\);
- 17M.1.sl.TZ1.4c.ii: Write down \(n(W \cap S)\).
- 17M.1.sl.TZ2.10a: Write down the probability that a light bulb produced by Home Shine is not defective.
- 17N.1.sl.TZ0.7c: Determine whether the events \(S\) and \(M\) are independent.
- 18M.2.sl.TZ1.2a: State the alternative hypothesis.
- 18M.2.sl.TZ1.5d.i: A contestant is chosen at random. Find the probability that this contestant fell into a trap...
- 18M.1.sl.TZ2.7b: Find the probability that the boy answered questions in Hindi.
- 18M.2.sl.TZ2.1c.i: Find the value of x.
- 18M.2.sl.TZ2.1d: Find the number of employees who, in the last year, did not travel to work by car, bicycle or...
- 10M.1.sl.TZ1.13a: Find the probability that a student chosen at random is male.
- 10M.1.sl.TZ2.8a: Find \({\text{P}}(A \cap B)\).
- 11N.1.sl.TZ0.10a: Write down the probability that (i) Ju Shen chooses a red disc from the bag; (ii) Ramón...
- 12N.2.sl.TZ0.4a: Use the table to find the probability that (i) a television will be bought by a...
- 12M.1.sl.TZ1.12b: Find the probability that Merryn will not be late for the concert.
- 10M.2.sl.TZ2.1a.i: Write down the value of a.
- 09M.1.sl.TZ1.11c: Find the probability that the number shown on the four-sided die is greater than the number...
- 11M.2.sl.TZ1.2B.a: One of the survey forms was chosen at random, find the probability that the form showed...
- 10M.2.sl.TZ2.1a.ii: Write down the value of b.
- 13N.1.sl.TZ0.7a: Complete the tree diagram.
- 14M.2.sl.TZ1.2d: There were 25 tourists in the group and every tourist saw at least one of the three types of...
- 15M.2.sl.TZ2.1f: The number of customers that like only mangoes is equal to the number of customers that like...
- 16N.1.sl.TZ0.12b: Find the value of \(p\).
- 16M.2.sl.TZ1.2c: i) On your Venn diagram, shade the set \({\left( {F \cup M} \right) \cap B'}\) . Do not...
- 16N.2.sl.TZ0.2b: Show that \(x = 3\).
- 17M.1.sl.TZ1.7a: Complete the tree diagram.
- 17M.1.sl.TZ2.10c: Write down an expression, in terms of \(a\), for the probability that at least one of...
- 17N.2.sl.TZ0.4e: Find the probability that the liquid turns blue.
- 18M.2.sl.TZ1.2b: Calculate the expected frequency of flights travelling at most 500 km and arriving slightly...
- 18M.2.sl.TZ1.2d.ii: Write down the associated p-value.
- 18M.2.sl.TZ1.5b: Find the probability that only one of Ayako and Natsuko falls into a trap while attempting to...
- 18M.1.sl.TZ2.7a: State the number of boys who answered questions in Portuguese.
- 10M.1.sl.TZ1.13c: Find the probability that a student chosen at random studies Physics, given that the student...
- 10N.1.sl.TZ0.6a: Write down the probability that this person is a smoker.
- 12M.2.sl.TZ1.2g: One student is chosen at random from the 120 students. Find the probability that this...
- 11N.2.sl.TZ0.2a: A student is chosen at random from the group. Find the probability that the student (i) ...
- 09M.1.sl.TZ2.13b: The die is thrown once. Given that the face on top is not red, find the probability that it...
- 13M.1.sl.TZ1.5a: Complete the tree diagram below.
- SPM.2.sl.TZ0.5d: Two students are chosen at random from all \(50\) students. Find the probability that(i) ...
- 07M.2.sl.TZ0.5i.b: Neil often takes the dogs to the park after they have eaten. He has noticed that the grey dog...
- 07N.2.sl.TZ0.1i.c: Find the probability that Geraldine is late.
- 08N.1.sl.TZ0.2d: One student is chosen at random from the group. Find the probability that this student...
- 13N.2.sl.TZ0.3e: Find the probability that a woman selected at random from the group had visited Europe.
- 13N.2.sl.TZ0.3f: Find the probability that a woman selected at random from the group had visited Europe, given...
- 16M.1.sl.TZ2.5a: Two friends, Sensen and Cruz, are conducting an investigation on probability. Sensen has a...
- 16M.1.sl.TZ1.1b: Find the probability that Nikita wins a match.
- 16M.2.sl.TZ1.2a: A group of students at Dune Canyon High School were surveyed. They were asked which of the...
- 16M.2.sl.TZ1.2d: A student who was surveyed is chosen at random. Find the probability that (i) the...
- 16M.2.sl.TZ1.2e: Dune Canyon High School has 850 students. Find the expected number of students at Dune...
- 17N.1.sl.TZ0.7a: Complete the Venn diagram for these students.
- 17N.2.sl.TZ0.4g: Estimate the number of employees, from this 38, who are allergic to nuts.
- 18M.2.sl.TZ1.2e: State, with a reason, whether you would reject the null hypothesis.
- 18M.2.sl.TZ2.1b.i: Use the tree diagram to find the probability that an employee encountered traffic and was...
- 18M.2.sl.TZ2.1b.iii: Use the tree diagram to find the probability that an employee encountered traffic given that...
- 10M.1.sl.TZ1.13b: Find the probability that a student chosen at random is either male or studies Chemistry.
- 10N.2.sl.TZ0.1A.f: Two students are chosen at random. Find the probability that both students had all three...
- 12M.2.sl.TZ2.1c: Leanne notices that on windy days, the probability she catches a fish is 0.1 while on...
- 12M.2.sl.TZ2.1f: Use your answer to part (e) to calculate the probability that Leanne catches a fish on two...
- 09N.1.sl.TZ0.9b: Find the probability that it does not snow tomorrow and Chuck is late for school.
- 09M.1.sl.TZ2.10a: If events A and B are mutually exclusive, write down the value of \({\text{P}} (A\cap B)\).
- 11M.1.sl.TZ2.9a: One traveller is to be chosen at random from all those interviewed. Find the probability...
- 11M.1.sl.TZ2.9c: One traveller is to be chosen at random from those not going to America. Find the...
- SPM.2.sl.TZ0.5c: Tomoko used a bus to travel to school yesterday. Find the probability that she also walked.
- 08N.2.sl.TZ0.3c: Two drivers are chosen at random. Calculate the probability that (i) both wear a seat...
- 08M.1.sl.TZ2.14b: Find the probability that Andy loses the point.
- 14M.2.sl.TZ1.2c: There were 25 tourists in the group and every tourist saw at least one of the three types of...
- 15M.1.sl.TZ1.11c: For a different day, also chosen at random, find the probability that, given Peter was late,...
- 14N.2.sl.TZ0.2c: Sonya, a lab assistant, counts the number of paths that lead to traps or escape doors. She...
- 16M.1.sl.TZ1.1a: The probability that Nikita wins a tennis match depends on the surface of the tennis court on...
- 16M.2.sl.TZ1.2b: Calculate the number of students who were surveyed.
- 16M.2.sl.TZ2.1a: \(180\) people were interviewed and asked what types of transport they had used in the...
- 16M.2.sl.TZ2.1b: Find the number of people who, in the last year, had travelled by (i) bus only; (ii) ...
- 16M.2.sl.TZ2.1c: A person is selected at random from those who were interviewed. Find the probability that...
- 16N.2.sl.TZ0.2c: Write down the value of \(n(B \cap C)\).
- 17M.1.sl.TZ1.4d: Write down, in terms of \(F\), \(W\) and \(S\), an expression for the set which contains only...
- 17M.1.sl.TZ1.7b: Find the probability that Sara’s baggage arrives in London.
- 17M.1.sl.TZ2.2a: Write down an expression, in terms of \(x\), for the number of children who play only...
- 17N.2.sl.TZ0.4c: Copy and complete the tree diagram.
- 18M.1.sl.TZ1.10b: Find the value of x.
- 18M.2.sl.TZ1.2c: Write down the number of degrees of freedom.
- 18M.1.sl.TZ2.7c: Two girls are selected at random. Calculate the probability that one girl answered questions...

