| Date | May 2014 | Marks available | 2 | Reference code | 14M.2.sl.TZ2.1 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Calculate | Question number | 1 | Adapted from | N/A |
Question
Tomek is attending a conference in Singapore. He has both trousers and shorts to wear. He also has the choice of wearing a tie or not.
The probability Tomek wears trousers is \(0.3\). If he wears trousers, the probability that he wears a tie is \(0.8\).
If Tomek wears shorts, the probability that he wears a tie is \(0.15\).
The following tree diagram shows the probabilities for Tomek’s clothing options at the conference.
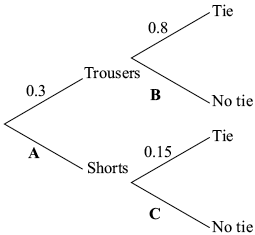
Find the value of
(i) \({\text{A}}\);
(ii) \({\text{B}}\);
(iii) \({\text{C}}\).
Calculate the probability that Tomek wears
(i) shorts and no tie;
(ii) no tie;
(iii) shorts given that he is not wearing a tie.
The conference lasts for two days.
Calculate the probability that Tomek wears trousers on both days.
The conference lasts for two days.
Calculate the probability that Tomek wears trousers on one of the days, and shorts on the other day.
Markscheme
(i) \(0.7 \left( {\frac{{70}}{{100}},{\text{ }}\frac{7}{{10}},{\text{ 70% }}} \right)\) (A1)
(ii) \(0.2 \left( {\frac{{20}}{{100}},{\text{ }}\frac{2}{{10}},{\text{ }}\frac{1}{5},{\text{ 20% }}} \right)\) (A1)
(iii) \(0.85 \left( {\frac{{85}}{{100}},{\text{ }}\frac{{17}}{{20}},{\text{ 85% }}} \right)\) (A1)
[3 marks]
(i) \(0.7 \times 0.85\) (M1)
Note: Award (M1) for multiplying their values from parts (a)(i) and (a)(iii).
\( = 0.595{\text{ }}\left( {\frac{{119}}{{200}},{\text{ 59.5% }}} \right)\) (A1)(ft)(G1)
Note: Follow through from part (a).
(ii) \(0.3 \times 0.2 + 0.7 \times 0.85\) (M1)(M1)
Note: Award (M1) for their two products, (M1) for adding their two products.
\( = 0.655{\text{ }}\left( {\frac{{131}}{{200}},{\text{ 65.5% }}} \right)\) (A1)(ft)(G2)
Note: Follow through from part (a).
(iii) \(\frac{{0.595}}{{0.655}}\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for correct numerator, (A1)(ft) for correct denominator. Follow through from parts (b)(i) and (ii).
\( = 0.908{\text{ }}\left( {{\text{0.90839}} \ldots ,{\text{ }}\frac{{119}}{{131}},{\text{ 90,8% }}} \right)\) (A1)(ft)(G2)
[8 marks]
\(0.3 \times 0.3\) (M1)
\( = 0.09 \left( {\frac{9}{{100}}, 9\%} \right)\) (A1)(G2)
[2 marks]
\(0.3 \times 0.7\) (M1)
\(0.3 \times 0.7 \times 2\) OR \((0.3 \times 0.7) + (0.7 \times 0.3)\) (M1)
Note: Award (M1) for their correct product seen, (M1) for multiplying their product by 2 or for adding their products twice.
\( = 0.42 \left( {\frac{{42}}{{100}}, \frac{{21}}{{50}}, 42\%} \right)\) (A1)(ft)(G2)
Note: Follow through from part (a)(i).
[3 marks]

