| Date | November 2016 | Marks available | 4 | Reference code | 16N.2.sl.TZ0.2 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
A group of 66 people went on holiday to Hawaii. During their stay, three trips were arranged: a boat trip (\(B\)), a coach trip (\(C\)) and a helicopter trip (\(H\)).
From this group of people:
| 3 | went on all three trips; |
| 16 | went on the coach trip only; |
| 13 | went on the boat trip only; |
| 5 | went on the helicopter trip only; |
| x | went on the coach trip and the helicopter trip but not the boat trip; |
| 2x | went on the boat trip and the helicopter trip but not the coach trip; |
| 4x | went on the boat trip and the coach trip but not the helicopter trip; |
| 8 | did not go on any of the trips. |
One person in the group is selected at random.
Draw a Venn diagram to represent the given information, using sets labelled \(B\), \(C\) and \(H\).
Show that \(x = 3\).
Write down the value of \(n(B \cap C)\).
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
Markscheme
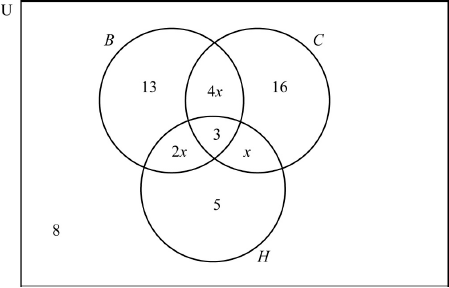 (A5)
(A5)
Notes: Award (A1) for rectangle and three labelled intersecting circles (U need not be seen),
(A1) for 3 in the correct region,
(A1) for 8 in the correct region,
(A1) for 5, 13 and 16 in the correct regions,
(A1) for \(x\), \(2x\) and \(4x\) in the correct regions.
[5 marks]
\(8 + 13 + 16 + 3 + 5 + x + 2x + 4x = 66\) (M1)
Note: Award (M1) for either a completely correct equation or adding all the terms from their diagram in part (a) and equating to 66.
Award (M0)(A0) if their equation has no \(x\).
\(7x = 66 - 45\) OR \(7x + 45 = 66\) (A1)
Note: Award (A1) for adding their like terms correctly, but only when the solution to their equation is equal to 3 and is consistent with their original equation.
\(x = 3\) (AG)
Note: The conclusion \(x = 3\) must be seen for the (A1) to be awarded.
[2 marks]
15 (A1)(ft)
Note: Follow through from part (a). The answer must be an integer.
[1 mark]
(i) \(\frac{{42}}{{66}}{\text{ }}\left( {\frac{7}{{11}},{\text{ }}0.636,{\text{ }}63.6\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram.
(ii) \(\frac{3}{9}{\text{ }}\left( {\frac{1}{3},{\text{ }}0.333,{\text{ }}33.3\% } \right)\) (A1)(A1)(ft)(G2)
Note: Award (A1) for numerator, (A1)(ft) for denominator. Follow through from their Venn diagram.
[4 marks]

