| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ1.11 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 11 | Adapted from | N/A |
Question
Peter either walks or cycles to work. The probability that he walks is 0.25. If Peter walks to work, the probability that he is late is 0.1. If he cycles to work, the probability that he is late is 0.05. The tree diagram for this information is shown.
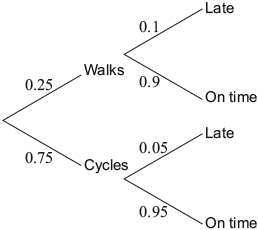
On a day chosen at random, Peter walked to work.
Write down the probability that he was on time.
For a different day, also chosen at random,
find the probability that Peter cycled to work and was late.
For a different day, also chosen at random,
find the probability that, given Peter was late, he cycled to work.
Markscheme
\(0.9\) (A1) (C1)
\(0.75 \times 0.05\) (M1)
\( = 0.0375\;\;\;\left( {\frac{3}{{80}},{\text{ 3,75% }}} \right)\) (A1) (C2)
\(\frac{{0.75 \times 0.05}}{{0.75 \times 0.05 + 0.25 \times 0.1}}\) (M1)(M1)
Note: Award (M1) for their correct numerator, (M1) for their correct denominator, ie, \(\left( {\frac{{{\text{their (b)}}}}{{{\text{their (b)}} + 0.25 \times 0.1}}} \right)\).
Do not award (M1) for their \(0.0375\) or \(0.0625\) if not a correct part of a fraction.
\( = 0.6\;\;\;\left( {\frac{3}{5},{\text{ }}60\% } \right)\) (A1)(ft) (C3)
Note: Follow through from part (b).
Examiners report
Surprisingly, in part (a) the majority of candidates answered incorrectly. The usual answer was 0.225, resulting from 0.25 × 0.9; the probability that Peter walks and arrives on time.
In part (b) the answers were mostly correct as the candidates repeated the same procedure, which was correct for this part.
The conditional probability in part (c) was too much for most. In some cases a correct numerator or denominator was found. More candidates could have received method marks if working had been shown.

