| Date | November 2017 | Marks available | 2 | Reference code | 17N.1.sl.TZ0.7 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
Rosewood College has 120 students. The students can join the sports club (\(S\)) and the music club (\(M\)).
For a student chosen at random from these 120, the probability that they joined both clubs is \(\frac{1}{4}\) and the probability that they joined the music club is\(\frac{1}{3}\).
There are 20 students that did not join either club.
Complete the Venn diagram for these students.
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.
Determine whether the events \(S\) and \(M\) are independent.
Markscheme
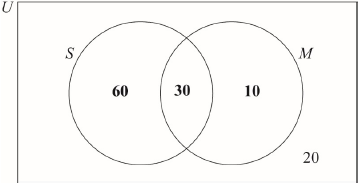(A1)(A1) (C2)
Note: Award (A1) for 30 in correct area, (A1) for 60 and 10 in the correct areas.
[2 marks]
\(\frac{{30}}{{90}}{\text{ }}\left( {\frac{1}{3},{\text{ }}0.333333 \ldots ,{\text{ }}33.3333 \ldots \% } \right)\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for correct numerator of 30, (A1)(ft) for correct denominator of 90. Follow through from their Venn diagram.
[2 marks]
\({\text{P}}(S) \times {\text{P}}(M) = \frac{3}{4} \times \frac{1}{3} = \frac{1}{4}\) (R1)
Note: Award (R1) for multiplying their by \(\frac{1}{3}\).
therefore the events are independent \(\left( {{\text{as P}}(S \cap M) = \frac{1}{4}} \right)\) (A1)(ft) (C2)
Note: Award (R1)(A1)(ft) for an answer which is consistent with their Venn diagram.
Do not award (R0)(A1)(ft).
Do not award final (A1) if \({\text{P}}(S) \times {\text{P}}(M)\) is not calculated. Follow through from part (a).
[2 marks]
