| Date | November 2014 | Marks available | 3 | Reference code | 14N.2.sl.TZ0.2 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
Mike, the laboratory mouse, is placed at the starting point, S, of a maze. Some paths in the maze lead to Trap A, some to Trap B, and others to escape doors. Some paths have one and some have two sections. If his path forks, Mike randomly chooses a path forward.
The following tree diagram represents the maze, showing all possible paths, and the probability that Mike chooses a certain section of a path through the maze.
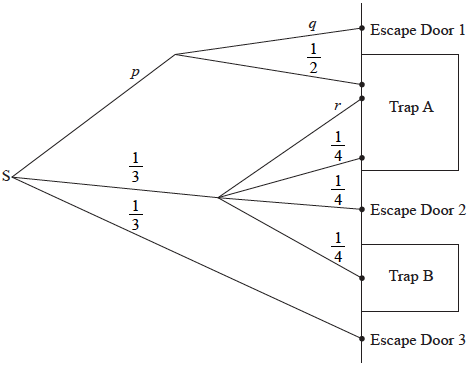
Write down the value of
(i) \(p\) ;
(ii) \(q\) ;
(iii) \(r\).
(i) Find the probability that Mike reaches Trap B.
(ii) Find the probability that Mike reaches Trap A.
(iii) Find the probability that Mike escapes from the maze.
Sonya, a lab assistant, counts the number of paths that lead to traps or escape doors. She believes that the probability that Mike will be trapped is greater than the probability that he will escape.
State whether Sonya is correct. Give a mathematical justification for your conclusion.
During the first trial Mike escapes.
Given that Mike escaped, find the probability that he went directly from S to Escape Door 3.
Markscheme
(i) \(\frac{1}{3}\;\;\;(0.333333…,{\text{ }}33.3333...\% )\) (A1)
(ii) \(\frac{1}{2}\;\;\;(0.5,{\text{ }}50\% )\) (A1)
(iii) \(\frac{1}{4}\;\;\;(0.25,{\text{ }}25\% )\) (A1)
(i) \(\frac{1}{3} \times \frac{1}{4}\) (M1)
\( = \frac{1}{{12}}\;\;\;({\text{0.0833333..., 8.33333...% )}}\) (A1)(G2)
(ii) \(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{4}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their three correct products seen, (M1) for addition of their products.
\( = \frac{1}{3}\;\;\;(0.333333...,{\text{ }}33.3333...\% )\) (A1)(ft)(G2)
Note: Follow through from their parts (a)(i) and (a)(iii).
(iii) \(1 - \frac{1}{{12}} - \frac{1}{3}\) (M1)
Note: Follow through from parts (b)(i) and (b)(ii).
OR
\(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3}\) (M1)
Note: Follow through from parts (a)(i) and (a)(ii).
\( = \frac{7}{{12}}\;\;\;(0.583333...,{\text{ }}58.3333...\% )\) (A1)(ft)(G2)
Sonya is not correct. (A1)(ft)
The probability that Mike escapes is \(\frac{7}{{12}}\), which is
greater than \(\frac{5}{{12}}{\text{ }}\left( {{\text{or greater than }}\frac{1}{2}} \right)\). (R1)(ft)
Notes: Do not award (A1)(R0).
Follow through from their answers to part (b).
\(\frac{{\frac{1}{3}}}{{\frac{7}{{12}}}}\) (A1)(A1)(ft)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
\( = \frac{4}{7}\;\;\;\left( {\frac{{12}}{{21}},{\text{ 0.571428..., 57.1428...% }}} \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (b)(iii).

