| Date | November 2017 | Marks available | 6 | Reference code | 17N.2.sl.TZ0.10 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Note: In this question, distance is in millimetres.
Let \(f(x) = x + a\sin \left( {x - \frac{\pi }{2}} \right) + a\), for \(x \geqslant 0\).
The graph of \(f\) passes through the origin. Let \({{\text{P}}_k}\) be any point on the graph of \(f\) with \(x\)-coordinate \(2k\pi \), where \(k \in \mathbb{N}\). A straight line \(L\) passes through all the points \({{\text{P}}_k}\).
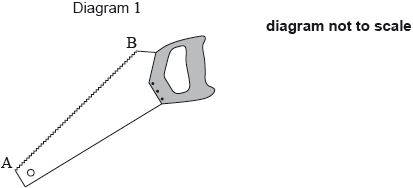
Diagram 1 shows a saw. The length of the toothed edge is the distance AB.
The toothed edge of the saw can be modelled using the graph of \(f\) and the line \(L\). Diagram 2 represents this model.
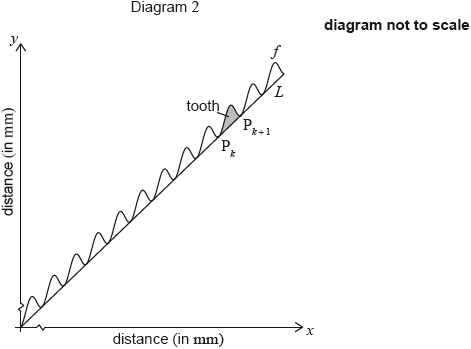
The shaded part on the graph is called a tooth. A tooth is represented by the region enclosed by the graph of \(f\) and the line \(L\), between \({{\text{P}}_k}\) and \({{\text{P}}_{k + 1}}\).
Show that \(f(2\pi ) = 2\pi \).
Find the coordinates of \({{\text{P}}_0}\) and of \({{\text{P}}_1}\).
Find the equation of \(L\).
Show that the distance between the \(x\)-coordinates of \({{\text{P}}_k}\) and \({{\text{P}}_{k + 1}}\) is \(2\pi \).
A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.
Markscheme
substituting \(x = 2\pi \) M1
eg\(\,\,\,\,\,\)\(2\pi + a\sin \left( {2\pi - \frac{\pi }{2}} \right) + a\)
\(2\pi + a\sin \left( {\frac{{3\pi }}{2}} \right) + a\) (A1)
\(2\pi - a + a\) A1
\(f(2\pi ) = 2\pi \) AG N0
[3 marks]
substituting the value of \(k\) (M1)
\({{\text{P}}_0}(0,{\text{ }}0),{\text{ }}{{\text{P}}_1}(2\pi ,{\text{ }}2\pi )\) A1A1 N3
[3 marks]
attempt to find the gradient (M1)
eg\(\,\,\,\,\,\)\(\frac{{2\pi - 0}}{{2\pi - 0}},{\text{ }}m = 1\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{y - 2\pi }}{{x - 2\pi }} = 1,{\text{ }}b = 0,{\text{ }}y - 0 = 1(x - 0)\)
y = x A1 N3
[3 marks]
subtracting \(x\)-coordinates of \({{\text{P}}_{k + 1}}\) and \({{\text{P}}_k}\) (in any order) (M1)
eg\(\,\,\,\,\,\)\(2(k + 1)\pi - 2k\pi ,{\text{ }}2k\pi - 2k\pi - 2\pi \)
correct working (must be in correct order) A1
eg\(\,\,\,\,\,\)\(2k\pi + 2\pi - 2k\pi ,{\text{ }}\left| {2k\pi - 2(k + 1)\pi } \right|\)
distance is \(2\pi \) AG N0
[2 marks]
METHOD 1
recognizing the toothed-edge as the hypotenuse (M1)
eg\(\,\,\,\,\,\)\({300^2} = {x^2} + {y^2}\), sketch
correct working (using their equation of \(L\) (A1)
eg\(\,\,\,\,\,\)\({300^2} = {x^2} + {x^2}\)
\(x = \frac{{300}}{{\sqrt 2 }}\) (exact), 212.132 (A1)
dividing their value of \(x\) by \(2\pi {\text{ }}\left( {{\text{do not accept }}\frac{{300}}{{2\pi }}} \right)\) (M1)
eg\(\,\,\,\,\,\)\(\frac{{212.132}}{{2\pi }}\)
33.7618 (A1)
33 (teeth) A1 N2
METHOD 2
vertical distance of a tooth is \(2\pi \) (may be seen anywhere) (A1)
attempt to find the hypotenuse for one tooth (M1)
eg\(\,\,\,\,\,\)\({x^2} = {(2\pi )^2} + {(2\pi )^2}\)
\(x = \sqrt {8{\pi ^2}} \) (exact), 8.88576 (A1)
dividing 300 by their value of \(x\) (M1)
eg
33.7618 (A1)
33 (teeth) A1 N2
[6 marks]

