| Date | May 2012 | Marks available | 2 | Reference code | 12M.1.sl.TZ2.3 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows the graph of \(f(x) = a\cos (bx)\) , for \(0 \le x \le 4\) .
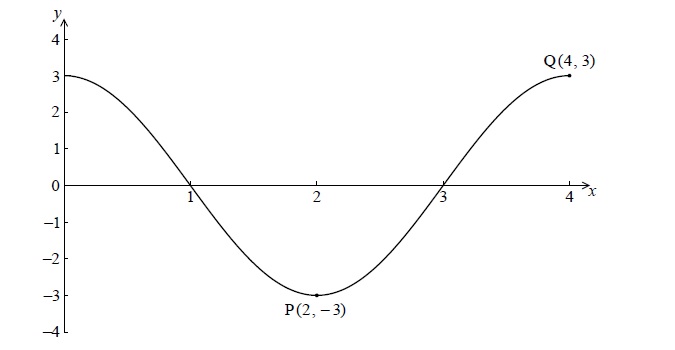
There is a minimum point at P(2, − 3) and a maximum point at Q(4, 3) .
(i) Write down the value of a .
(ii) Find the value of b .
Write down the gradient of the curve at P.
Write down the equation of the normal to the curve at P.
Markscheme
(i) \(a = 3\) A1 N1
(ii) METHOD 1
attempt to find period (M1)
e.g. 4 , \(b = 4\) , \(\frac{{2\pi }}{b}\)
\(b = \frac{{2\pi }}{4}\left( { = \frac{\pi }{2}} \right)\) A1 N2
[3 marks]
METHOD 2
attempt to substitute coordinates (M1)
e.g. \(3\cos (2b) = - 3\) , \(3\cos (4b) = 3\)
\(b = \frac{{2\pi }}{4}\left( { = \frac{\pi }{2}} \right)\) A1 N2
[3 marks]
0 A1 N1
[1 mark]
recognizing that normal is perpendicular to tangent (M1)
e.g. \({m_1} \times {m_2} = - 1\) , \(m = - \frac{1}{0}\) , sketch of vertical line on diagram
\(x = 2\) (do not accept 2 or \(y = 2\) ) A1 N2
[2 marks]
Examiners report
In part (a), many candidates were able to successfully write down the value of a as instructed by inspecting the graph and seeing the amplitude of the function is 3. Many also used a formulaic approach to reach the correct answer. When finding the value of b, there were many candidates who thought b was the period of the function, rather than \(\frac{{2\pi }}{{{\rm{period}}}}\) .
In part (b), the directions asked candidates to write down the gradient of the curve at the local minimum point P. However, many candidates spent a good deal of time finding the derivative of the function and finding the value of the derivative for the given value of x, rather than simply stating that the gradient of a curve at a minimum point is zero.
For part (c), finding the equation of the normal to the curve, many candidates tried to work with algebraic equations involving negative reciprocal gradients, rather than recognizing that the equation of the vertical line was \(x = 2\) . There were also candidates who had trouble expressing the correct equation of a line parallel to the y-axis.

