| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.sl.TZ1.8 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
At Grande Anse Beach the height of the water in metres is modelled by the function \(h(t) = p\cos (q \times t) + r\), where \(t\) is the number of hours after 21:00 hours on 10 December 2017. The following diagram shows the graph of \(h\) , for \(0 \leqslant t \leqslant 72\).
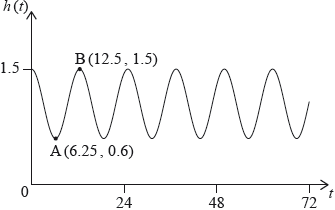
The point \({\text{A}}(6.25,{\text{ }}0.6)\) represents the first low tide and \({\text{B}}(12.5,{\text{ }}1.5)\) represents the next high tide.
How much time is there between the first low tide and the next high tide?
Find the difference in height between low tide and high tide.
Find the value of \(p\);
Find the value of \(q\);
Find the value of \(r\).
There are two high tides on 12 December 2017. At what time does the second high tide occur?
Markscheme
attempt to find the difference of \(x\)-values of A and B (M1)
eg\(\,\,\,\,\,\)\(6.25 - 12.5{\text{ }}\)
6.25 (hours), (6 hours 15 minutes) A1 N2
[2 marks]
attempt to find the difference of \(y\)-values of A and B (M1)
eg\(\,\,\,\,\,\)\(1.5 - 0.6\)
\(0.9{\text{ (m)}}\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} - {\text{min}}}}{2},{\text{ }}0.9 \div 2\)
\(p = 0.45\) A1 N2
[2 marks]
METHOD 1
period \( = 12.5\) (seen anywhere) (A1)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({\text{period}} = \frac{{2\pi }}{b},{\text{ }}q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{12.5}}\)
0.502654
\(q = \frac{{4\pi }}{{25}},{\text{ 0.503 }}\left( {{\text{or }} - \frac{{4\pi }}{{25}},{\text{ }} - 0.503} \right)\) A1 N2
METHOD 2
attempt to use a coordinate to make an equation (M1)
eg\(\,\,\,\,\,\)\(p\cos (6.25q) + r = 0.6,{\text{ }}p\cos (12.5q) + r = 1.5\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(0.45\cos (6.25q) + 1.05 = 0.6,{\text{ }}0.45\cos (12.5q) + 1.05 = 1.5\)
0.502654
\(q = \frac{{4\pi }}{{25}},{\text{ }}0.503{\text{ }}\left( {{\text{or }} - \frac{{4\pi }}{{25}},{\text{ }} - 0.503} \right)\) A1 N2
[3 marks]
valid method to find \(r\) (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} + {\text{min}}}}{2},{\text{ }}0.6 + 0.45\)
\(r = 1.05\) A1 N2
[2 marks]
METHOD 1
attempt to find start or end \(t\)-values for 12 December (M1)
eg\(\,\,\,\,\,\)\(3 + 24,{\text{ }}t = 27,{\text{ }}t = 51\)
finds \(t\)-value for second max (A1)
\(t = 50\)
23:00 (or 11 pm) A1 N3
METHOD 2
valid approach to list either the times of high tides after 21:00 or the \(t\)-values of high tides after 21:00, showing at least two times (M1)
eg\(\,\,\,\,\,\)\({\text{21:00}} + 12.5,{\text{ 21:00}} + 25,{\text{ }}12.5 + 12.5,{\text{ }}25 + 12.5\)
correct time of first high tide on 12 December (A1)
eg\(\,\,\,\,\,\)10:30 (or 10:30 am)
time of second high tide = 23:00 A1 N3
METHOD 3
attempt to set their \(h\) equal to 1.5 (M1)
eg\(\,\,\,\,\,\)\(h(t) = 1.5,{\text{ }}0.45\cos \left( {\frac{{4\pi }}{{25}}t} \right) + 1.05 = 1.5\)
correct working to find second max (A1)
eg\(\,\,\,\,\,\)\(0.503t = 8\pi ,{\text{ }}t = 50\)
23:00 (or 11 pm) A1 N3
[3 marks]

