| Date | May 2008 | Marks available | 3 | Reference code | 08M.1.sl.TZ1.4 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Sketch | Question number | 4 | Adapted from | N/A |
Question
Consider \(g(x) = 3\sin 2x\) .
Write down the period of g.
On the diagram below, sketch the curve of g, for \(0 \le x \le 2\pi \) .
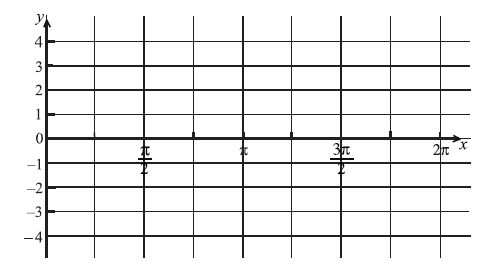
Write down the number of solutions to the equation \(g(x) = 2\) , for \(0 \le x \le 2\pi \) .
Markscheme
\({\text{period}} = \pi \) A1 N1
[1 mark]
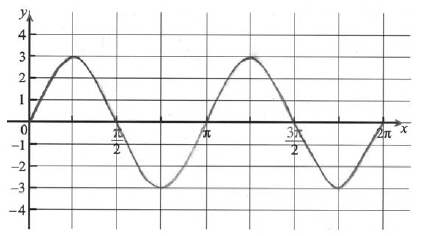 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for amplitude of 3, A1 for their period, A1 for a sine curve passing through \((0{\text{, }}0)\) and \((0{\text{, }}2\pi )\) .
[3 marks]
evidence of appropriate approach (M1)
e.g. line \(y = 2\) on graph, discussion of number of solutions in the domain
4 (solutions) A1 N2
[2 marks]
Examiners report
Many candidates were unable to write down the period of the function.
Many candidates were unable to write down the period of the function. However, they were often then able to go and correctly sketch the graph with the correct period.
The final part was poorly done with many candidates finding the number of zeros instead of the intersection with the line \(y = 2\) .

