| Date | May 2010 | Marks available | 6 | Reference code | 10M.1.sl.TZ1.6 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
The graph of \(f(x) = \sqrt {16 - 4{x^2}} \) , for \( - 2 \le x \le 2\) , is shown below.
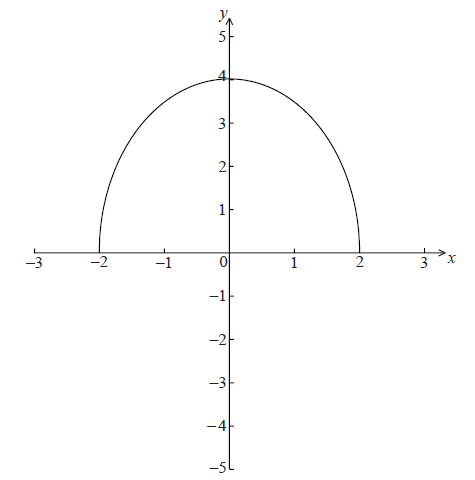
The region enclosed by the curve of f and the x-axis is rotated \(360^\circ \) about the x-axis.
Find the volume of the solid formed.
Markscheme
attempt to set up integral expression M1
e.g. \(\pi {\int {\sqrt {16 - 4{x^2}} } ^2}{\rm{d}}x\) , \(2\pi \int_0^2 {(16 - 4{x^2})} \) , \({\int {\sqrt {16 - 4{x^2}} } ^2}{\rm{d}}x\)
\(\int {16} {\rm{d}}x = 16x\) , \(\int {4{x^2}{\rm{d}}x = } \frac{{4{x^3}}}{3}\) (seen anywhere) A1A1
evidence of substituting limits into the integrand (M1)
e.g. \(\left( {32 - \frac{{32}}{3}} \right) - \left( { - 32 + \frac{{32}}{3}} \right)\) , \(64 - \frac{{64}}{3}\)
volume \(= \frac{{128\pi }}{3}\) A2 N3
[6 marks]
Examiners report
Many candidates correctly integrated using \(f(x)\) , although some neglected to square the function and mired themselves in awkward integration attempts. Upon substituting the limits, many were unable to carry the calculation to completion. Occasionally the \(\pi \) was neglected in a final answer. Weaker candidates considered the solid formed to be a sphere and did not use integration.

