| Date | November 2010 | Marks available | 3 | Reference code | 10N.2.sl.TZ0.2 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Sketch | Question number | 2 | Adapted from | N/A |
Question
The velocity v ms−1 of an object after t seconds is given by \(v(t) = 15\sqrt t - 3t\) , for \(0 \le t \le 25\) .
On the grid below, sketch the graph of v , clearly indicating the maximum point.
(i) Write down an expression for d .
(ii) Hence, write down the value of d .
Markscheme
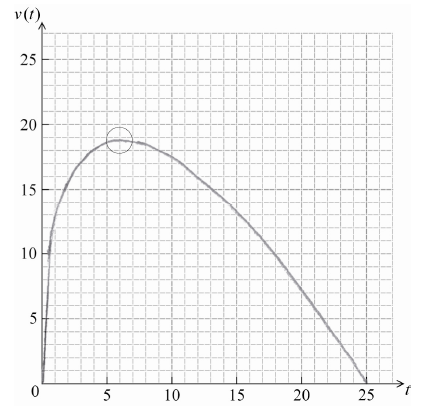 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately correct shape, A1 for right endpoint at \((25{\text{, }}0)\) and A1 for maximum point in circle.
[3 marks]
(i) recognizing that d is the area under the curve (M1)
e.g. \(\int {v(t)} \)
correct expression in terms of t, with correct limits A2 N3
e.g. \(d = \int_0^9 {(15\sqrt t } - 3t){\rm{d}}t\) , \(d = \int_0^9 v {\rm{d}}t\)
(ii) \(d = 148.5\) (m) (accept 149 to 3 sf) A1 N1
[4 marks]
Examiners report
The graph in part (a) was well done. It was pleasing to see many candidates considering the domain as they sketched their graph.
Part (b) (i) asked for an expression which bewildered a great many candidates. However, few had difficulty obtaining the correct answer in (b) (ii).

