| Date | May 2017 | Marks available | 6 | Reference code | 17M.2.sl.TZ2.7 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Justify and Find | Question number | 7 | Adapted from | N/A |
Question
Note: In this question, distance is in metres and time is in seconds.
A particle moves along a horizontal line starting at a fixed point A. The velocity \(v\) of the particle, at time \(t\), is given by \(v(t) = \frac{{2{t^2} - 4t}}{{{t^2} - 2t + 2}}\), for \(0 \leqslant t \leqslant 5\). The following diagram shows the graph of \(v\)
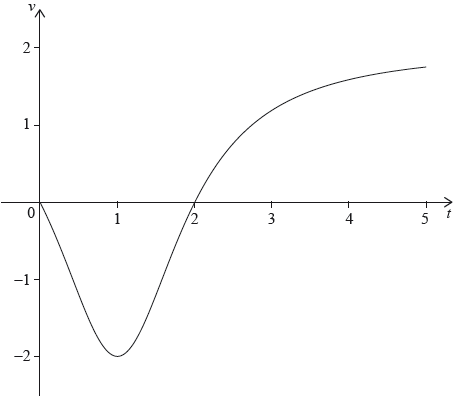
There are \(t\)-intercepts at \((0,{\text{ }}0)\) and \((2,{\text{ }}0)\).
Find the maximum distance of the particle from A during the time \(0 \leqslant t \leqslant 5\) and justify your answer.
Markscheme
METHOD 1 (displacement)
recognizing \(s = \int {v{\text{d}}t} \) (M1)
consideration of displacement at \(t = 2\) and \(t = 5\) (seen anywhere) M1
eg\(\,\,\,\,\,\)\(\int_0^2 v \) and \(\int_0^5 v \)
Note: Must have both for any further marks.
correct displacement at \(t = 2\) and \(t = 5\) (seen anywhere) A1A1
\( - 2.28318\) (accept 2.28318), 1.55513
valid reasoning comparing correct displacements R1
eg\(\,\,\,\,\,\)\(\left| { - 2.28} \right| > \left| {1.56} \right|\), more left than right
2.28 (m) A1 N1
Note: Do not award the final A1 without the R1.
METHOD 2 (distance travelled)
recognizing distance \( = \int {\left| v \right|{\text{d}}t} \) (M1)
consideration of distance travelled from \(t = 0\) to 2 and \(t = 2\) to 5 (seen anywhere) M1
eg\(\,\,\,\,\,\)\(\int_0^2 v \) and \(\int_2^5 v \)
Note: Must have both for any further marks
correct distances travelled (seen anywhere) A1A1
2.28318, (accept \( - 2.28318\)), 3.83832
valid reasoning comparing correct distance values R1
eg\(\,\,\,\,\,\)\(3.84 - 2.28 < 2.28,{\text{ }}3.84 < 2 \times 2.28\)
2.28 (m) A1 N1
Note: Do not award the final A1 without the R1.
[6 marks]

