| Date | May 2014 | Marks available | 4 | Reference code | 14M.1.sl.TZ1.3 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
Let \(f(x) = {x^2}\).
Find \(\int_1^2 {{{\left( {f(x)} \right)}^2}{\text{d}}x} \).
The following diagram shows part of the graph of \(f\).
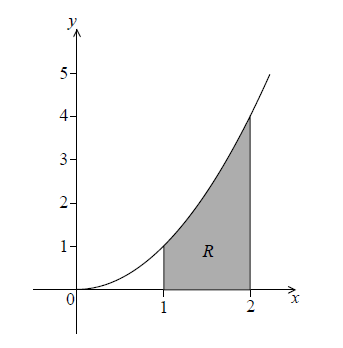
The shaded region \(R\) is enclosed by the graph of \(f\), the \(x\)-axis and the lines \(x = 1\) and \(x = 2\).
Find the volume of the solid formed when \(R\) is revolved \({360^ \circ }\) about the \(x\)-axis.
Markscheme
substituting for \({\left( {f(x)} \right)^2}\) (may be seen in integral) A1
eg \({\left( {{x^2}} \right)^2}{\text{, }}{x^4}\)
correct integration, \(\int {{x^4}{\text{d}}x = \frac{1}{5}{x^5}} \) (A1)
substituting limits into their integrated function and subtracting (in any order) (M1)
eg \(\frac{{{2^5}}}{5} - \frac{1}{5}{\text{, }}\frac{1}{5}(1 - 4)\)
\(\int_1^2 {{{\left( {f(x)} \right)}^2}{\text{d}}x} = \frac{{31}}{5}( = 6.2) \) A1 N2
[4 marks]
attempt to substitute limits or function into formula involving \({f^2}\) (M1)
eg \(\int_1^2 {{{\left( {f(x)} \right)}^2}{\text{d}}x{\text{, }}\pi \int {{x^4}{\text{d}}x} } \)
\(\frac{{31}}{5}\pi {\text{ }}( = 6.2\pi )\) A1 N2
[2 marks]

